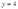1一个竞争性的利润最大化厂商有利润函数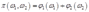 。将产出价格正规化,令其等于1。
。将产出价格正规化,令其等于1。
(a)对函数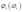 求一阶导数和二阶导数,可以得到什么结论?
求一阶导数和二阶导数,可以得到什么结论?
(b)如果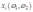 是对要素
是对要素 的要素需求函数,
的要素需求函数,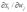 的符号是什么?
的符号是什么?
(c)令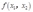 为产生这种形式的利润函数的生产函数。这种生产函数的形式是什么样子的?(提示:参见一阶条件)
为产生这种形式的利润函数的生产函数。这种生产函数的形式是什么样子的?(提示:参见一阶条件)
A competitive profit-maximizing firm has a profit function 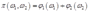 .The price of output is normalized to be 1.
.The price of output is normalized to be 1.
(a)What do we know about the first and second derivatives of the functions 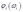 ?
?
(b)If 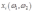 is the factor demand function for factor
is the factor demand function for factor  , what is the sign of
, what is the sign of 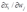 ?
?
(c)Let 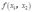 be the production function?(Hint:look at the first-order conditions.)
be the production function?(Hint:look at the first-order conditions.)
答:(a)由利润函数的凸性得到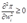 ,从而可知
,从而可知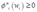 ;又因为利润函数关于要素价格是单减的,即
;又因为利润函数关于要素价格是单减的,即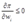 ,从而可知
,从而可知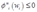 。
。
(b)根据Hotelling引理可知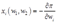 ,因此
,因此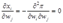 。
。
(c)由(b)可知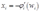 ,又因为对
,又因为对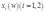 ,
,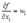 恒成立。
恒成立。
从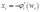 中反解出
中反解出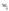 代入上式中可知
代入上式中可知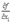 只和
只和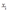 有关;同理可知
有关;同理可知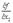 只和
只和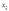 有关,从而可知
有关,从而可知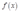 一定可以写成如下形式:
一定可以写成如下形式: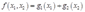 。
。
2考虑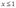 ,
,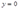 和
和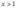 ,
,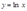 所描述的技术。计算出这种技术的利润函数。
所描述的技术。计算出这种技术的利润函数。
Consider the technology described by 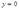 for
for 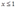 and
and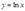 for
for 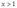 . Calculate the profit function for this technology.
. Calculate the profit function for this technology.
解:令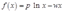 ,易知
,易知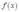 在区间
在区间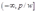 上单增,在区间
上单增,在区间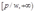 上单减,所以
上单减,所以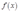 在
在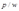 这一点上达到最大值。下面分情况讨论:
这一点上达到最大值。下面分情况讨论:
(1)当 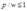 时,如果厂商停产,那么它的利润就是零;如果厂商继续生产,那么当它的产量为1时,可以得到最高利润为
时,如果厂商停产,那么它的利润就是零;如果厂商继续生产,那么当它的产量为1时,可以得到最高利润为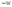 。所以,厂商的最优选择就是不生产。
。所以,厂商的最优选择就是不生产。
(2)当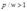 时,如果厂商停产,那么它的利润就是零;如果厂商继续生产,那么当它的产量为
时,如果厂商停产,那么它的利润就是零;如果厂商继续生产,那么当它的产量为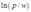 时,可以得到最高利润,为
时,可以得到最高利润,为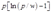 。所以如果
。所以如果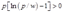 即
即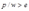 时,厂商应当选择生产
时,厂商应当选择生产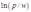 数量的产品,相应的利润为
数量的产品,相应的利润为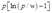 ;如果
;如果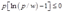 ,那么厂商应当选择停产,此时的利润为零。
,那么厂商应当选择停产,此时的利润为零。
综上可知,厂商的利润函数为:
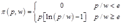
如图3-1所示。
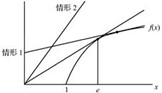
图3-1 厂商的利润最大化
3给出生产函数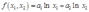 ,计算出利润最大化的需求和供给函数,以及利润函数。为简单起见,假定存在内解。假定
,计算出利润最大化的需求和供给函数,以及利润函数。为简单起见,假定存在内解。假定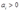 。
。
Given the production function 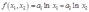 ,calculate the profit-maximizing demand and supply functions,and the profit function. For simplicity assume an interior solution. Assume that
,calculate the profit-maximizing demand and supply functions,and the profit function. For simplicity assume an interior solution. Assume that 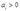 .
.
解:利润最大化问题:

一阶条件为:
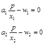
得出要素需求方程为: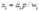 ,
,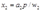 。
。
将要素需求方程代入生产函数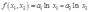 ,得到供给函数:
,得到供给函数:
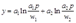
将要素需求方程代入目标函数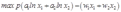 就得出利润函数:
就得出利润函数:
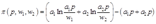
4给出生产函数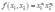 ,计算出利润最大化的需求和供给函数,以及利润函数,假定
,计算出利润最大化的需求和供给函数,以及利润函数,假定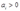 。
。 和
和
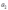
必须满足什么样的约束?
Given the production function 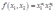 ,calculate the profit-maximizing demand and supply functions, and the profit function. Assume
,calculate the profit-maximizing demand and supply functions, and the profit function. Assume 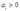 . What restrictions must
. What restrictions must  and
and 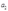 satisfy?
satisfy?
解:利润最大化问题: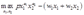
一阶条件是:
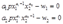
解得要素需求函数:
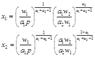
将要素需求函数代入目标函数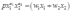 即求得利润函数:
即求得利润函数:
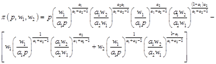
当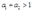 时,生产函数规模报酬递增,所以不存在最大利润;当
时,生产函数规模报酬递增,所以不存在最大利润;当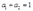 时,得到柯布—道格拉斯生产函数,所以不存在最大利润;当
时,得到柯布—道格拉斯生产函数,所以不存在最大利润;当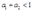 时,优化问题的海赛矩阵负定,所以存在最大利润。
时,优化问题的海赛矩阵负定,所以存在最大利润。
综上可知 时,利润最大化问题有解。
时,利润最大化问题有解。
5给出生产函数 ,计算出利润最大化的需求和供给函数,以及利润函数。
,计算出利润最大化的需求和供给函数,以及利润函数。 必须满足什么约束?
必须满足什么约束?
Given the production function  , calculate the profit -maximizing demand and supply functions, and the profit function. What restriction must a satisfy?
, calculate the profit -maximizing demand and supply functions, and the profit function. What restriction must a satisfy?
解:厂商的利润最大化问题为:
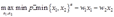
对于最优解必有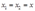 ,所以上述最优化问题可以化简为:
,所以上述最优化问题可以化简为:
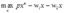
从而解得要素需求函数为:
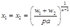
将要素需求函数代入生产函数得到供给函数:
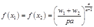
将要素需求函数代入目标函数得到利润函数:
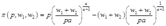
上述最优化问题的二阶条件为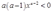 ,可见为了满足二阶条件必须有
,可见为了满足二阶条件必须有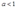 ;当
;当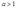 时,生产函数规模报酬递增,所以不存在最大利润;当
时,生产函数规模报酬递增,所以不存在最大利润;当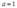 时,只有当
时,只有当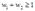 时,厂商有最大利润(等于零),当
时,厂商有最大利润(等于零),当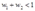 时,厂商无最大利润;综上可知:当
时,厂商无最大利润;综上可知:当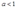 时,厂商的利润函数处处存在。
时,厂商的利润函数处处存在。
1严格证明利润最大化意味着成本最小化。
Prove rigorously that profit maximization implies cost minimization.
证明:令 为价格
为价格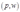 下利润最大化的一个投入向量。这意味着,对于所有可允许的
下利润最大化的一个投入向量。这意味着,对于所有可允许的 ,
, 必须满足
必须满足
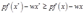
。
假设对于产出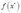 ,
, 没有使成本最小化,即存在一个向量
没有使成本最小化,即存在一个向量 满足
满足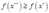 与w
与w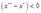 ,因而在
,因而在 下所取得的利润必须大于在
下所取得的利润必须大于在 下所取得的利润:
下所取得的利润:
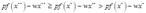
这与 使利润最大化的假设相矛盾,故假设不成立,因此利润最大化意味着成本最小化。
使利润最大化的假设相矛盾,故假设不成立,因此利润最大化意味着成本最小化。
2使用库恩-塔克定理得出即使最优解涉及边界解时也是正确的成本最小化条件。
Use the Kuhn-Tucker theorem to derive conditions for cost minimization that are valid even if the optimal solution involves a boundary solution.
答:互补—松弛条件为:
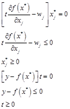
当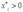 和
和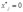 成立时,上式就隐含着:
成立时,上式就隐含着:
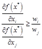
这个不等式意味着用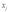 代替
代替 时,可以降低成本,然而由于企业已经用完了它可以得到的
时,可以降低成本,然而由于企业已经用完了它可以得到的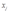 的所有数量,所以继续降低成本是不可能的。
的所有数量,所以继续降低成本是不可能的。
3一个厂商有两个车间,它们各自的成本函数为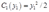 和
和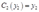 。该厂商的成本函数是什么?
。该厂商的成本函数是什么?
A firm has two plants with cost functions 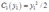 and
and 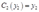 .What is the cost function for the firm?
.What is the cost function for the firm?
解:厂商的成本最小化问题为:
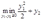
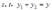
从约束条件中解出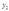 的表达式,然后代入目标函数式中得到:
的表达式,然后代入目标函数式中得到:
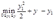
下面分情况讨论:
(1)如果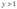 ,那么
,那么 的最优值为1,此时的成本函数为
的最优值为1,此时的成本函数为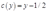 。
。
(2)如果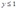 ,那么
,那么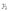 的最优值为
的最优值为 ,此时的成本函数为
,此时的成本函数为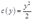 。
。
4一个厂商有两个车间。一个车间根据生产函数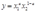 来生产产出,另一个厂车间的生产函数是
来生产产出,另一个厂车间的生产函数是
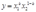
。该技术的成本函数是什么?
A firm has two plants. One plant produces output according to the production function 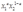 .The other plant has a production function
.The other plant has a production function 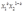 .What is the cost function for this technology?
.What is the cost function for this technology?
答:考虑柯布-道格拉斯技术的成本函数的成本最小化问题(以第一个车间的生产函数为例):
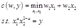
将上述问题转化为无约束问题:
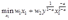
一阶条件为:
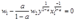
得到要素需求函数:
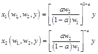
将要素需求函数代入到目标函数中:

其中,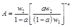 。
。
因此第一个车间的成本函数为: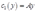 ,则第二个车间的成本函数为:
,则第二个车间的成本函数为: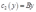 ,其中,
,其中,
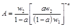 ,
,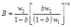 。
。
如果厂商采用成本最低的生产方法进行生产,则该厂商的生产成本函数为:

即让平均成本低的工厂生产所有的产量。
5假定厂商有两种可能的方式来生产产出。方式a:使用 单位的物品1和
单位的物品1和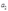 单位的物品2来生产1单位的产出。方式b:使用
单位的物品2来生产1单位的产出。方式b:使用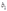 单位的物品1和
单位的物品1和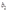 单位的物品2来生产1单位的产出。要素只能以这些固定比例使用。如果要素价格是
单位的物品2来生产1单位的产出。要素只能以这些固定比例使用。如果要素价格是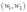 ,对这两种要素的需求是什么?该技术的成本函数是什么?对什么样的要素价格,成本函数是不可微的?
,对这两种要素的需求是什么?该技术的成本函数是什么?对什么样的要素价格,成本函数是不可微的?
Suppose that the firm has two possible activities to produce output. Activity a uses  units of good 1 and
units of good 1 and 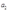 units of good 2 to produce 1 unit of output. Activity b uses
units of good 2 to produce 1 unit of output. Activity b uses 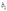 units of good 1 and
units of good 1 and 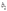 units of good 2 to produce 1 unit of output. Factors can only be used in these fixed proportions. If the factor prices are
units of good 2 to produce 1 unit of output. Factors can only be used in these fixed proportions. If the factor prices are 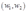 , what are the demands for the two factors? What is the cost function for this technology? For what factor prices is the cost function not differentiable?
, what are the demands for the two factors? What is the cost function for this technology? For what factor prices is the cost function not differentiable?
答:生产函数为:
方式a: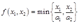
方式b: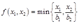
用方式a生产1单位产品的成本是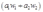 ,用方式b生产1单位产品的成本是
,用方式b生产1单位产品的成本是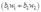 。这样如果厂商计划生产
。这样如果厂商计划生产 单位的产量,那么它会使用成本较低的那种生产方式生产全部产品,从而厂商的成本函数为:
单位的产量,那么它会使用成本较低的那种生产方式生产全部产品,从而厂商的成本函数为:

要素1的需求函数由下式给出:

要素2的需求函数由下式给出:

当 时,成本函数将是不可微的。
时,成本函数将是不可微的。
6一个厂商有两个车间,成本函数分别是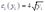 和
和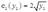 。生产
。生产 的产出,它的成本是多少?
的产出,它的成本是多少?
A firm has two plants with cost functions 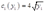 and
and 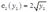 . What is its cost of producing an output y?
. What is its cost of producing an output y?
解:企业的成本最小化问题为:
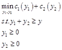
这个问题的拉格朗日函数为:
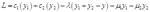
这里 、
、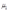 、
、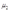 都是非负的。库恩-塔克条件为:
都是非负的。库恩-塔克条件为:
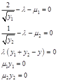
下面分情况讨论:
①最优解为内部解的情况:此时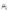 、
、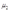 都等于零,这就意味着:
都等于零,这就意味着:
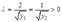
 大于零又意味着
大于零又意味着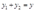 ,从而解得:
,从而解得:
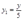 ,
,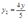 ,
,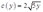
②最优解为角解的情况:此时若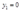 ,那么:
,那么:
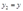 ,
,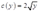
可见角解优于内部解。若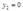 时,
时,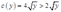 ,故这种情况舍去。
,故这种情况舍去。
综上可知,厂商的成本函数为:
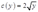
7表4-1显示了对一个厂商的要素需求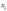 、
、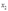 ,要素价格
,要素价格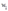 、
、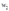 和产出
和产出 的两组观测值。表中所描述的行为与成本最小化行为一致吗?
的两组观测值。表中所描述的行为与成本最小化行为一致吗?
Table 4-1 shows two observations on factor demand 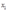 ,
, 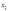 , factor prices,
, factor prices, 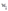 ,
, 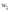 , and output,
, and output,  for a firm. Is the behavior depicted in this table consistent with cost-minimizing behavior?
for a firm. Is the behavior depicted in this table consistent with cost-minimizing behavior?
表4-1 要素的价格,投入数量和产出数量的关系

答:表中所描述的行为与成本最小化行为不一致。理由如下:成本最小化行为意味着成本最小化弱公理成立,即:
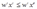 ,对任意的
,对任意的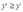
现在生产100单位产出花费的成本为: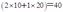 ,但在同一价格下,生产110单位的产出花费的成本仅为:
,但在同一价格下,生产110单位的产出花费的成本仅为:
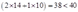
这就和成本最小化弱公理相矛盾.
8一个厂商有生产函数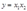 。如果在
。如果在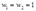 时,生产的最小成本等于4,
时,生产的最小成本等于4, 等于什么?
等于什么?
A firm has a production function 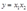 .If the minimum cost of production at
.If the minimum cost of production at 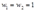 is equal to 4, what is
is equal to 4, what is

equal to?
解:企业的成本最小化问题:
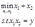 (1)
(1)
将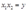 代入目标函数,得出无约束最小化问题:
代入目标函数,得出无约束最小化问题:
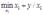 (2)
(2)
其一阶条件是:
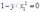 (3)
(3)
得到:
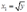 (4)
(4)
同理有:
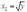 (5)
(5)
将(4)式和(5)式代入目标函数中,得到成本函数为: 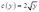 ,根据已知条件最小成本为4,即:
,根据已知条件最小成本为4,即: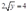 ,解得:
,解得: