浙江工商大学830运筹学考研真题及辅导用书

考研真题

1. 浙江工商大学管理工程与电子商务学院（含现代商贸研究中心）《830运筹学》历年考研真题汇总（含部分答案）

2. 全国名校运筹学考研真题汇总（含部分答案）

考研指导书

1. 胡运权《运筹学教程》（第5版）配套题库【考研真题精选＋课后习题＋章节题库】

浙江工商大学管理工程与电子商务学院（含现代商贸研究中心）《830运筹学》历年考研真题汇总（含部分答案）

书籍目录

部分内容

2011年浙江工商大学《830运筹学》考研真题

招生专业：管理科学与工程

考试科目：830运筹学

一、填空题（每个空格3分，共30分）

1在单纯形法中，初始基可能由决策变量、______、______ 三种类型的变量组成。

2线性规划的可行域是一个______，若其有最优解，必能在______上获得。

3如线性规划原问题有可行解且目标函数值无界，则其对偶问题______。

4对于3个产地4个销地的产销平衡运输问题，其基变量的个数是______个；其中决策变量x₂₃所对应的列向量P₂₃ =______。

5在目标规划中，如果要求某个目标约束恰好等于其期望值，则其目标函数应该为极小化______。

6在动态规划中，______表明了一个阶段到下一阶段状态转移规律。

7在任何图中，次（度）为奇数的顶点数目必为______。

二、计算题（共50分）

1已知线性规划的数学模型为：

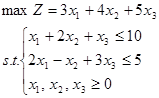
问题：

(1) 用单纯形法求该模型的最优解。(8分)

(2) 当第一个约束条件变为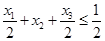时，问题的最优解如何变化？(7分)

2已知线性规划的数学模型为：

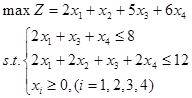
问题：

(1)写出其对偶问题。(7分)

(2)已知其对偶问题最优解Y^*=(4, 1)，试用对偶理论求原问题的最优解。（3分）

3试求解下面极小化指派问题：（10分）

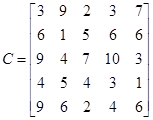
4求下图中A到F的最短路：（15分）

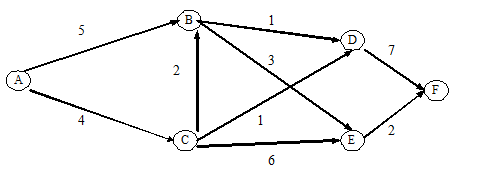
三、应用题（共60分）

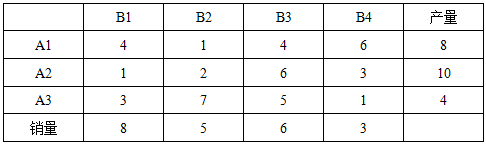
1某地区有三个化肥厂A1，A2，A3生产某种化肥，该地区有四个产粮区B1，B2，B3和B4需要该化肥。各化肥厂的产量、各产粮区的销量和各化肥厂运往各产粮区每吨化肥的运价（元）如下表所示。问应如何调运，可使总运费最小？（15分）

2某厂生产A、B、C三种电子产品，装配工作在同一条生产线上完成。三种产品的装配时间分别为6、8、10小时，生产线每月正常工作时间为200小时；三种产品的月销售预计为12、10、6台，每台销售利润分别为500、650、800元。该厂拟按以下目标制定每月的生产计划：

第一目标：利润超过16000元；

第二目标：充分利用生产能力；

第三目标：加班时间不超过24小时；

第四目标：产量不低于预计销量；

第五目标：B产品产量不能超过A产品；

请建立该目标规划的数学模型（不要求求解）。（15分）

3某鞋店出售橡胶雪靴，预计未来4个月市场需求量如下，每次订货只有10、20、30、40、50几种，每种批量的价格为48、86、118、138、160元，每月末库存不能超过40双，存贮费用按月末计算，每双0.2元，考虑到四个月后市场风险较大，希望四个月后的库存为0，这四个月如何订货，总花费最小。（15分）

4某油田A向炼油厂B输送原油，输油管及最大容量如下图所示，试求最大流量。（15分）

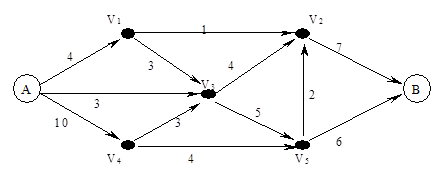
四、证明题（共10分）

对于约束为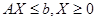的极大化线性规划问题，设其最优基为B，其对应的价值系数为C_B，证明该线性规划问题的对偶问题的最优解为。

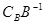更多内容，请点击获取：
http://shuyue.100xuexi.com/Ebook/971440.html