北京邮电大学813管理工程基础考研真题及辅导用书

考研真题

1. 北京邮电大学《813管理工程基础》历年考研真题汇总（含部分答案）

2. 全国名校管理学考研真题汇总

3. 全国名校运筹学考研真题汇总（含部分答案）

考研指导书

1. 周三多《管理学》（第5版）笔记和课后习题（含考研真题）

2. 周三多《管理学》（第5版）配套题库【考研真题精选＋章节题库】

3. 胡运权《运筹学教程》（第5版）配套题库【考研真题精选＋课后习题＋章节题库】

北京邮电大学《813管理工程基础》历年考研真题汇总（含部分答案）

书籍目录

部分内容

2003年北京邮电大学《419管理基础》考研真题

北京邮电大学2003年硕士研究生入学考试试题

科目：419管理基础

一、问答题

1名词解释（每个小题3分，共18分）：

（1）消费者剩余

（2）外部性

（3）有效需求

（4）JIT

（5）帕金森定律

（6）权变理论

2举例说明以下概念的区别（每个小题3分，共18分）：

（1）LAN、WAN、MAN

（2）职能部、事业部

（3）权益性资本、债务型资本

（4）风险决策、不确定决策

（5）X理论、Y理论

（6）计划、决策

3简答题（每个小题5分，共20分）：

（1）管理的两重性及二者的关系。

（2）TQC与ISO 9000的关系。

（3）组织设计的任务是什么，原则有哪些?

（4）贝尔曼最优性原理。

二、分析题

4在一个小镇上已经有两家啤酒屋，其中一个以廉价闻名，另一个则以高档和特色啤酒来吸引顾客，如果你决定开设第三家啤酒屋，那么你的市场定位是什么，为什么（5分）?

5请画出波士顿矩阵的示意图，并解释如何根据矩阵进行决策分析（5分）。

6试用麦克尔·波特行业竞争结构分析图分析我国固定电话市场状况（9分）。

三、计算题

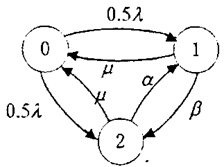
7求右面线性规划的最优解，并给出资源A和B的影子价。（15分）

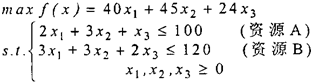
8有一线性规划，原问题为目标函数为max型，有三个决策变量，其第一行约束为≤型，对应松弛变量为x₄，其第二行约束为≥型，对应剩余变量为x₅，其第三行约束为≤型，对应松弛变量为x₆。下面是其最优单纯形表，求：

（1）c₂的灵敏度范围（5分）。

（2）△b₁，△b₂的灵敏度范围（10分）。

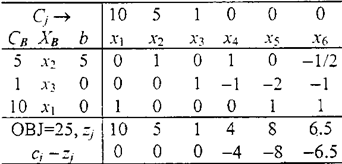
9如下边的网络图（每边上标的是流量f_ij），我们希望简化该网络结构（即删去一些流量小的边），一般可采用限界值法，即给定一个值V，若f_ij<V以则删去边e_ij。显然，y大到一定程度就会使网络不连通。

（1）采用系统的算法求使网络保持连通的最大限界值V_max（采用试凑法或穷举法不给分，即你的算法应可以适用很大的网络）；（10分）

（2）证明你的算法满足题目的要求（5分）。

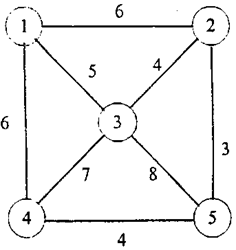
10某排队系统的稳态状态转移图如下图，试推导该系统的稳态概率（15分）。

11有给定厚度的金属板材28m²，通过裁剪可焊接成如图的封闭的长方体。设该长方体可承受的压力F与图中三个面的面积x₁，x₂，x₃有如下关系：

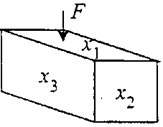
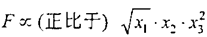
求最优的裁剪方案使F最大。（设任何裁剪方案都无余料）

（1）建立该问题的数学模型（7分）。

（2）用连续型的动态规划方法求最优方案（8分）。

更多内容，请点击获取：
http://shuyue.100xuexi.com/Ebook/970858.html