1一项试验有3个步骤,第1步有3种可能的结果,第2步有2种可能的结果,第3步有4种可能的结果。则整个试验总共有多少种可能的结果?
答:整个试验总共可能的结果=3×2×4=24。
2一个项目组包含6个项目,从中任取3项,共有多少种取法?以字母A、B、C、D、E、F来分别表示这6项,试列出所有可能的3项组合。
解:(1) 。
。
(2)设A、B、C、D、E、F分别表示这6个项目,则所有可能的3项组合如表4-1所示。
表4-1

3一个项目组包含6个项目,从中任取3项,共有多少种排列方法?以字母A、B、C、D、E、F来分别表示这6项,试列出由B、D和F组成的所有排列。
解:a. 。
。
b.B、D和F组成的所有排列为:BDF、BFD、DBF、DFB、FBD和FDB。
4考虑一个将硬币抛掷3次的试验。
a.画出试验的树形图。
b.列出试验的各种结果。
c.计算每种试验结果的概率。
解:设抛掷硬币时出现正面记为H,出现反面记为T。
a.试验的树形图如图4-1所示。
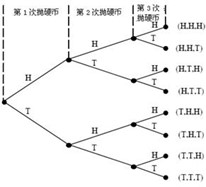
图4-1 抛掷3次硬币的树形图
b.试验的各种结果为(H,H,H),(H,H,T),(H,T,H),(H,T,T),(T,H,H),(T,H,T),(T,T,H),(T,T,T)。
c.由于试验的各种结果总共为8个,因此由古典法可知,每个试验结果的概率均为1/8。
5假定试验有5种等可能的结果:E1、E2、E3、E4、E5。求每种试验结果的概率并证明满足式(4-3)和式(4-4)中的两个基本前提。你采用何种方法?
解:a.由于E1、E2、E3、E4、E5是等可能发生的,所以其概率为
 ,i=1,2,3,4,5
,i=1,2,3,4,5
b.显然
 ,i=1,2,3,4,5
,i=1,2,3,4,5

采用的是古典法。
6某项试验有3种结果:E1、E2和E3。现将该试验重复50次,其中E1出现20次,E2出现13次,E3出现17次。求每种试验结果的概率。你采用何种方法?
解: ,
, ,
,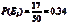
采用的是相对频数法。
7某决策者给出了一项试验的4种结果的主观概率:P(E1)=0.1、P(E2)=0.15、P(E3)=0.4和P(E4)=0.2。试问这些概率的分配合理吗?解释原因。
解:这些概率的分配并不合理。
由于
P(E1)+ P(E2)+ P(E3)+ P(E4)=0.1+0.15+0.4+0.2=0.85
此等式不满足概率分配的基本条件 。
。
8在Milford市,改变市区划分的申请要经过一个两步骤的程序:由计划委员会审议,由市政委员会最终决定。在第l步,计划委员会对改变市区划分的要求进行审议后,提出有关支持或反对的意见。在第2步,市政委员会对计划委员会的意见进行投票,以批准或否决对市区划分的改变。现在某房地产开发商已经递交了一份要求改变市区划分的申请。将申请程序视为一项试验。
a.在这个试验中有多少个样本点?列出各样本点。
b.画出试验的树形图。
解:a.在这个试验中有4个样本点。分别为:计划委员会支持—市政委员会批准,计划委员会支持—市政委员会否决,计划委员会反对—市政委员会批准,计划委员会反对—市政委员会否决。
b.令p=计划委员会支持,n=计划委员会反对,a=市政委员会批准,d=市政委员会否决。则试验的树形图如图4-2所示。

图4-2 试验的树形图
9简单随机抽样就是从容量为N的总体中抽取容量为n的样本,利用样本数据来推断总体特征。假设我们有一个由50个银行账户构成的总体,并从中随机抽取4个作为样本用以推断总体特征。共有多少种不同的抽样结果?
解:不同的抽样结果的种数有:
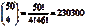
10近年来,对风险资本的有效使用极大地满足了企业对资金的需求。据VEnture Economics(Investor’s Business Daily,2000.4.28)统计,在1999年,共进行了2374笔风险资本支付。其中,有1434笔是支付给加利福尼亚州的企业,有390笔是支付给马萨诸塞州的企业,有217笔是支付给纽约州的企业,有112笔是支付给科罗拉多州的企业。在这些企业中,有20%的企业是在发展的早期阶段获得资金,有55%的企业是在扩张阶段获得的资金。假定从这些公司中随机抽取一个公司以了解它是如何使用这些资金的。试问:
a.所选出的公司来自加利福尼亚州的概率是多大?
b.所选出的公司不是来自题中所提及四个州的概率是多大?
c.所选出的公司不是在发展的早期阶段获得资金的概率是多大?
d.假定处于发展早期阶段的企业在美国是均匀分布的,则马萨诸塞州的企业在其发展的早期阶段得到多少风险资本基金?
e.假定基金的投资总额是32.4亿美元。试估计科罗拉多州企业所得到的数额。
解:a.采用相对频数法可得:
P(来自加利福尼亚州)=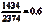
b.不是来自这四个州的资金笔数=2374-1434-390-217-112=221,所以
P(不是来自这四个州)=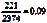
c.由于有20%的企业是在发展的早期阶段获得资金,所以
P(不是在发展的早期阶段获得资金)=1-0.20=0.80
d.马萨诸塞州的企业在其发展的早期阶段得到的风险资本基金的笔数=20%×390=78。
e.如果假设州与州之间得到的基金投资总额没有差异,则可以将科罗拉多州得到基金投资的概率与整个风险资本基金总额相乘得到估计值。即
科罗拉多州得到基金投资的估计值=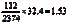 (亿美元)
(亿美元)

表4-2

解:a.由于NHTSA总共调查了1086(858+228)人,使用安全带的人数为858人,所以采用相对频数法可得:
P(使用安全带)=
b.由于2002年驾驶员使用安全带的概率是0.75,而在2003年使用安全带的概率达到0.79>0.78,所以NHTSA局长杰弗里 伦奇博士对调查的结果是满意的。
伦奇博士对调查的结果是满意的。
c.每个地区驾驶员使用安全带的概率分别为:
P(北部使用安全带)=
P(中部使用安全带)=
P(南部使用安全带)=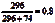
P(西部使用安全带)=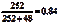
可见,西部地区驾驶员使用安全带的概率最高。
d.在此样本中,北部地区驾驶员所占比例是0.184(200/1086),中部地区驾驶员所占比例是0.199(216/1086),南部地区驾驶员所占比例是0.341(370/1086),西部地区驾驶员所占比例是0.276(300/1086)。
南部地区被选取的驾驶员最多,西部地区次之。
e.由于南部和西部地区驾驶员被选取的最多,并且这两个地区的驾驶员使用安全带的概率较高,所以在(a)中所得估计概率过高。

解:a.由组合计数法则可得被抽中的5个白球上的号码的不同组合的种数有:

b.获得200000美元的概率=1/3478761=0.000000287。
c.被抽中的5个白球和1个红球的组合数=3478761×42=146107962,所以获得强力球六合彩头奖的概率=1/146107962=0.0000000068。
13某个牙膏制造商研制了5种不同的外包装设计。假设每种设计被消费者选择的可能性都是相等的。那么你将如何为每种外包装设计分配概率?在一次实际试验中,有100名消费者被要求按其喜好来选择外包装设计,获得数据如下表。这些数据是否能够表明每种设计被选择的可能性是相等的?解释原因。
表4-3
| 外包装类型 |
被选择次数 |
外包装类型 |
被选择次数 |
| 1 |
5 |
4 |
40 |
| 2 |
15 |
5 |
10 |
| 3 |
30 |
|
|
答:假设每种设计被消费者选择的可能性都是相等的。那么每种外包装设计的概率为0.20。
表中数据不能够表明每种设计被选择的可能性是相等的。使用相对频数原则可以得出,选择外包装类型1的概率为0.05,选择外包装类型2的概率为0.15,选择外包装类型3的概率为0.30,选择外包装类型4的概率为0.40,选择外包装类型5的概率为0.10。
14某项试验有4种等可能发生的试验结果:E1、E2、E3和E4。
a.E2发生的概率是多少?
b.任意两种试验结果(如E1或E2)之一发生的概率是多少?
c.任意三种试验结果(如E1或E2或E4)之一发生的概率是多少?
解:a.由于E1、E2、E3,和E4 是等可能发生的,所以P(E2)=1/4。
b.P(任意两个试验结果)=1/4+1/4=1/2。
c.P(任意三种试验结果)=1/4+1/4+1/4=3/4。
15从52张扑克牌中任意抽取1张,每一张对应于一个概率为1/52的样本点。
a.对于事件”抽出的一张是A”,列出其样本点。
b.对于事件”抽出的一张是草花”,列出其样本点。
c.对于事件”抽出的一张是花脸儿(即J、Q或K)”,列出其样本点。
d.对于(a)、(b)、(c)中的事件,分别计算它们的概率。
解:a.S={方块A,红桃A,黑桃A,草花A}。
b.S={草花2,草花3,…,草花10,草花J,草花Q,草花K,草花A}。
c.S={方块J,方块Q,方块K,红桃J,红桃Q,红桃K,黑桃J,黑桃Q,黑桃K,草花J,草花Q,草花K}。
d.(a):P(抽出的一张是A)=4/52=0.08;
(b):P(抽出的一张是草花)=13/52=0.25;
(c):P(抽出的一张是花脸儿)=12/52=0.23。
16考虑投掷两枚骰子的试验,我们所关心的是两个骰子朝上一面的数值之和。
a.共有多少种可能的样本点?(提示:利用多步骤试验计数法则。)
b.列出样本点。
c.两个数之和为7的概率为多少?
d.两个数之和大于等于9的概率为多少?
e.由于可能的和数中有6个偶数(2,4,6,8,10,12),而只有5个奇数(3,5,7,9,11),则获得偶数的可能比奇数更大。你是否同意上述观点?试解释原因。
f.你使用什么方法来分配概率?
解:a.共有36种可能的样本点。
b.样本点列入图4-3的方框中。
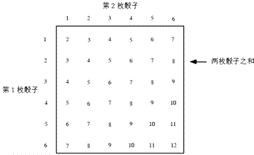
图4-3
c.由样本点可知,两个数之和为7的个数为6,所以P(两个数之和为7)=6/36=1/6。
d.由样本点可知,两个数之和大于9的个数为6,所以P(两个数之和大于9)=10/36=5/18。
e.不同意上述观点,因为获得奇数和偶数的概率相等,均为1/2。
f.由于各种实验结果是等概率发生的,所以会使用古典法来分配概率。
17参见KP&L公司问题的样本点及样本点的概率表。
a.如果设计阶段(阶段1)经过4个月才能完成,那么它就将超出预算。列出事件”设计阶段超出预算”的样本点。
b.设计阶段超出预算的概率是多少?
c.如果建设阶段(阶段2)经过8个月才能完成,那么它就将超出预算。列出事件”建设阶段超出预算”的样本点。
d.建设阶段超出预算的概率是多少?
e.两个阶段都超出预算的概率是多少?
解:a.事件”设计阶段超出预算”的样本点为(4,6),(4,7),(4,8)。
b.设计阶段超出预算的概率为:
P(4,6)+ P(4,7)+ P(4,8)=0.05+0.10+0.15=0.30
c.事件”建设阶段超出预算”的样本点为(2,8),(3,8),(4,8)。
d.建设阶段超出预算的概率为:
P(2,8)+ P(3,8)+ P(4,8)=0.05+0.05+0.15=0.25
e.两个阶段都超出预算的样本点为(4,8),所以其概率为:
P(4,8)=0.15
18假设小区的一名公寓管理人员对下个月空房数目所做的主观概率估计如表4-4所示。
表4-4

对于下面的事件,分别列出其样本点并计算事件的概率。
a.无空房。
b.至少有4间空房。
c.2间或2间以下空房。
解:a.样本点为0,P(0)=0.05。
b.样本点为4、5,P(4或者5)=0.1+0.1=0.2。
c.样本点为0、1、2,P(0、1或者2)=0.5+0.15+0.35=0.55。
19国家体育用品联合会对7岁及7岁以上的体育活动参与者进行了一项调查(Statistical Abstract of the United States:2002)。据统计,这一年龄组的人口总数为2.485亿,其中男性l.209亿,女性1.276亿。在所有项目中,参加者人数最多的前5项的数据如表4-5所示。
表4-5

求:
a.随机选一名女性,她参加以上各类项目的概率分别是多少?
b.随机选一名男性,他参加以上各类项目的概率分别是多少?
c.随机选一人,此人参加以上各类项目的概率分别是多少?
d.假如你恰好遇到一名竞走运动者从你身边走过,则此人是一名女性的概率为多大?此人是一男性的概率为多大?
解:a/b/c.利用相对频数法进行概率分配,对于每一项运动项目的人数分别除以男性和女性的总人数可得表4-6。
表4-6
| 活动项目 |
男性 |
女性 |
男性或女性 |
| 自行车 |
0.18 |
0.16 |
0.17 |
| 野营 |
0.21 |
0.19 |
0.20 |
| 徒步行走 |
0.24 |
0.45 |
0.35 |
| 器械练习 |
0.17 |
0.19 |
0.18 |
| 游泳 |
0.22 |
0.27 |
0.24 |
d.此人是一名女性的概率=
此人是一男性的概率=

表4-7
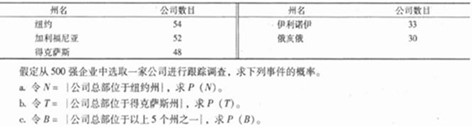
解:a.P(N)=54/500=0.108。
b.P(T)=48/500=0.096。
c.P(B)=217/500=0.434。
表4-8


解:美国人口的总人数=80.5+19.0+…+35.0=281.6,所以
a.P(年龄在20~24岁)=19.0/281.6=0.0674。
b.P(年龄在20~34岁)=(19.0+39.9)/281.6=0.2092。
c.P(年龄大于等于45岁)=(37.7+24.3+35.0)/281.6=0.3445。
22.假设我们有一个样本空间,它包含有5个等可能发生的试验结果:E1、E2、E3、E4、E5。令
A={E1,E2} B={E3,E4} C={E2,E3,E5}
a.求P(A)、P(B)和P(C)。
b.求P(A∪B)。A和B是否互斥?
c.求Ac、Cc、P(Ac)和P(Cc)。
d.求A∪Bc和P(A∪Bc)。
e.求P(B∪C)。
解:由于样本空间的事件是等可能发生的,所以
P(E1)=P(E2)=P(E3)=P(E4)=P(E5)=
a.P(A)= P(E1)+P(E2)=0.4;P(B)=P(E3)+P(E4)=0.4;P(C)=P(E2)+P(E3)+P(E5)=3/5=0.6。
b.由于A∩B= ,所以A和B是互斥的。P(A∪B)= P(A)+ P(B)=0.4+0.4=0.8。
,所以A和B是互斥的。P(A∪B)= P(A)+ P(B)=0.4+0.4=0.8。
c.Ac= { E3、E4、E5};Cc= { E1、E4};
P(Ac)=1-P(A)=1-0.4=0.6;P(Cc)= 1-P(C)=1-0.6=0.4。
d.A∪Bc={ E1,E2,E5}; P(A∪Bc)=0.6。
e.P(B∪C)= P(B)+P(C)-P(B∩C)=0.4+0.6-0.2=0.8。
23假设我们有一个样本空间S={E1,E2,E3,E4,E5,E6,E7},其中E1,E2,…,E7表示样本点。它们的概率分配如下:P(E1)=0.05,P(E2)=0.20,P(E3)=0.20,P(E4)=0.25,P(E5)=0.15,P(E6)=0.10,P(E7)=0.05。令
A={E1,E4,E6} B={E2,E4,E7} C={E2,E3,E5,E7}
a.求P(A)、P(B)和P(C)。
b.求A∪B和P(A∪B)。
c.求A∩B和P(A∩B)。
d.事件A和C是否互斥?
e.求Bc和P(Bc)。
解:a.P(A)=P(E1)+P(E4)+P(E6)=0.05+0.25+0.10=0.40;
P(B)=P(E2)+P(E4)+P(E7)=0.20+0.25+0.05=0.50;
P(C)=P(E2)+P(E3)+P(E5)+P(E7)=0.20+0.20+0.15+0.05=0.60。
b.A∪B={E1,E2,E4,E6,E7};
P(A∪B)=P(E1)+P(E2)+P(E4)+P(E6)+P(E7)
=0.05+0.20+0.25+0.10+0.05=0.65
c.A∩B={E4};P(A∩B)=P(E4)=0.25。
d.由于A∩B=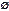 ,所以A和C是互斥的。
,所以A和C是互斥的。
e.BC={E1,E3,E5,E6};P(Bc)=P(E1)+P(E3)+P(E5)+P(E6)=0.05+0.20+0.15+0.10=0.50。
24Clarkson大学对毕业生进行了一项调查以了解他们对学校的看法。调查询问了受访者在学校的经历是未达到预期、达到预期还是超出预期。调查结果表明,有4%的人没有做出反应,有26%的人认为未达到预期,65%的人认为达到预期(Clarkson Magazine,2001年夏)。
a.如果我们随机选择一名毕业生,则他认为在学校的经历超出预期的概率为多少?
b.如果我们随机选择一名毕业生,则他认为在学校的经历达到或超出预期的概率为多少?
解:令E=经历超出预期,M=经历达到预期。
a.P(E)=100%-(4%+26%+65%)=5%。
b.P(M∪E)=P(M)+P(E)=0.65+0.05=0.70。

解:a.由于P(M)=0.56,P(F)=0.42,P(M∩F)=0.24,所以两位青年中至少有一位仍然与父母住在一起的概率为:
P(M∪F)=P(M)+P(F)-P(M∩F)=0.56+0.42-0.24=0.74
b.P(MC∩FC)=1-P(M∪F)=1-0.74=0.26,即这两位青年都单独住(都不与父母住在一起)的概率为0.26。
26《华尔街日报》公布了30家最大股票和对冲基金的1年期收益率和5年期收益率,截止日期为2000年3月31日(《华尔街日报》,2004.4.10)。假定我们称1年期收益率超过50%的基金为高收益,5年期收益率超过300%的基金为高收益。有9项基金的1年期收益率超过了50%,7项基金的5年期收益率超过了300%,有5项基金的1年期收益率超过了50%且5年期收益率超过了300%。现在,我们随机地选择一个基金。
a.求基金的1年期收益率为高收益率的概率,基金的5年期收益率为高收益率的概率。
b.基金的1年期和5年期收益率均为高收益率的概率。
c.求基金的1年期和5年期收益率均不为高收益率的概率。
解:令Y=1年期收益率为高收益率,M=5年期收益率为高收益率。
a.P(Y)=9/30=0.30,P(M)=7/30=0.23。
b.P(Y∩M)=5/30=0.17,即基金的1年期和5年期收益率均为高收益率的概率为0.17。
c.由于P(Y∪M)=0.30+0.23-0.17=0.36,所以
P(YC∩MC)=1-0.36=0.64
即基金的1年期和5年期收益率均不为高收益率的概率为0.64。
27在2001年NCAA足球的赛前民意测验中,其中的一个问题是:你认为Big Ten和Pac-10会进入本年度的”Rose Bowl”全国冠军杯决赛吗?在对13429名受访者的调查中,有2961人认为Big Ten会进入决赛,有4494人认为Pac-10会进入决赛,有6823人认为两队都不能进入决赛(www.yahoo.com,2001.8.30)。
a.受访者认为两队都不能进入决赛的概率为多少?
b.受访者认为两队中有一队进入决赛的概率为多少?
c.受访者认为两队都进入决赛的概率为多少?
解:由题中数据可得:
表4-9
| Big Ten | ||||
| 能 | 不能 | |||
| Pac-10 | 能 | 849 | 3645 | 4494 |
| 不能 | 2112 | 6823 | 8935 | |
| 2961 | 10468 | 13429 | ||
a.P(两队都不能进入决赛)= 。
。
b.P(两队中有一队进入决赛)= 。
。
c.P(两队都进入决赛)=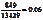 。
。
28某杂志对订阅者的调查表明,在过去12个月中45%的人由于工作原因而租赁汽车,54%的人由于个人原因而租赁汽车,30%的人既由于工作原因又由于个人原因而租赁汽车。
a.在过去12个月中,某订阅者因工作原因或个人原因而租赁汽车的概率是多少?
b.在过去12个月中,某订阅者既非因工作原因又非因个人原因而租赁汽车的概率是多少?
解:令B=由于工作原因而租赁汽车,P=由于个人原因而租赁汽车。
a.P(B∪P)=P(B)+P(P)-P(B∩P)=0.54+0.45-0.30=0.69
b.P(BC∩PC)=1-0.69=0.31
29每年有大量学习成绩优异的高中毕业生提前申请美国国内的名牌大学。有些大学由于生源相对稳定,拒绝学生提前申请。宾夕法尼亚大学共收到2851份这样的提前申请,其中有1033名学生的申请被接收,854名学生的申请被拒绝,964名学生待参加常规的招生考试后再做答复。据《今日美国》报道,宾夕法尼亚大学常规招生考试的录取率为18%,当年共招收包括提前申请的考生和参加正常招生考试的学生在内的考生2375名(USA Today,2001.1.24)。
令事件 A={学生通过常规招生考试被宾夕法尼亚大学录取}
E={学生通过提前申请被宾夕法尼亚大学录取}
R={学生提前申请直接被拒绝}
D={对学生的提前申请,宾夕法尼亚大学待其参加常规的招生考试后再做答复}
a.求事件E、R和D的概率。
b.事件E和D是否互斥?求P(E∩D)。
c.在被宾夕法尼亚大学录取的2375名学生中随机抽取一名学生,该生是提前申请获得录取的概率有多大?
d.假定一名学生向宾夕法尼亚大学提出提前申请,则该生在提前申请中获得录取或通过参加随后的常规招生考试后被录取的概率是多少?
解:a.P(E)=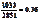 ;P(R)=
;P(R)= ;P(D)=
;P(D)= 。
。
b.事件E和D是互斥的,所以P(E∩D)=0。
c.该生是提前申请获得录取的概率= 。
。
d.964名参加常规的招生考试的学生中被录取的人数=964×0.18=174(人),在提前申请中获得录取或通过参加随后的常规招生考试后被录取的人数=1033+174=1207。所以
P(该生在提前申请或通过参加随后的常规招生考试后被录取)=1207/2851=0.42
30假设有两个事件A和B,P(A)=0.50,P(B)=0.60且P(A∩B)=0.40。
a.求P(A|B)。
b.求P(B|A)。
c.A和B是否独立?为什么?
解:a.
b.
c.由于P(A|B)P(A),所以A和B不是独立的。
31假设有两个事件A和B,它们是互斥的。并且我们已知P(A)=0.30,P(B)=0.40。
a.求P(A∩B)。
b.求P(A|B)。
c.某统计学专业的学生认为,互斥事件与独立事件的概念完全一样,并且如果两个事件是互斥的,则它们必然是独立的。你是否同意他的观点?利用本题的概率信息来印证你的答案。
d.根据本题的结果,你对互斥事件和独立事件有哪些一般性的结论?
解:a.由于事件A和B是互斥的,所以P(A∩B)=0。
b.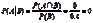
c.不同意他的观点,尽管事件A和B是互斥的,但是由于 ,所以他们并不是相互独立的。
,所以他们并不是相互独立的。
d.互斥事件并不是相互独立的。

表4-10

解:a.由表中数据可得:样本容量=750+950+170+130=2000,将表中数据分别处以2000可得联合概率分布表如表4-11所示。
表4-11 联合概率分布表
| |
健康保险 |
||
| 年龄 |
有 |
无 |
合计 |
| 18~34岁 |
0.375 |
0.085 |
0.46 |
| 35岁或以上 |
0.475 |
0.065 |
0.54 |
| 合计 |
0.850 |
0.150 |
1.00 |
令A=18~34岁,B=35岁或以上,Y=有健康保险,N=无健康保险。
b.由P(A)=0.46,P(B)=0.54可知,在18岁以上的美国人口中,18~34岁的人口占46%,35岁或以上的人口占54%。
c.P(N)=0.15
d.
e.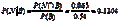
f.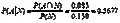
g.在美国18岁以上的人口中,没有健康保险的概率是0.15。在18~34岁的人口中没有保险的概率较高,为0.1848,近似为18.5%,而年龄34岁或以上的人口中,没有保险的概率为0.1204,近似为12%。在没有健康保险的人口中,18~34岁的人口占到0.5677,大约为57%。
33某大学毕业生管理委员会对MBA学生进行了一次调查,表4-12是关于”学生申请所投考学校的首要原因”的调查数据。
表4-12

a.根据上述数据求联合概率分布表。
b.利用学校质量、费用或便利和其他原因的边际概率来评述哪一项是选择学校的最主要因素。
c.如果某学生为全日制学生,则学校质量成为其选择学校的首要原因的概率为多少?
d.如果某学生为非全日制学生,则学校质量成为其选择学校的首要原因的概率为多少?
e.事件A表示某学生为全日制学生,事件B表示某学生将学校质量作为其选择学校的首要因素。试问事件A和事件B是否独立?说明你的理由。
解:a.由表中数据可得联合概率分布表,如表4-13所示。
表4-13 联合概率分布表
| |
|
申请原因 |
|
||
| |
|
学校质量 |
费用或便利 |
其他原因 |
合计 |
| 学生类型 | 全日制 |
0.218 |
0.204 |
0.039 |
0.461 |
| 非全日制 |
0.208 |
0.307 |
0.024 |
0.539 |
|
| 合计 |
0.426 |
0.511 |
0.063 |
1.00 |
|
b.由联合概率分布表可得,费用或便利的边际概率等于0.511,在所有的因素中是最大的,所以它是学生选择学校的最主要因素。学校质量的边际概率等于0.426,是学生选择学校的第二因素。
c.P(质量|全日制)=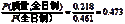
d.P(质量|非全日制)=
e.令A=全日制,B=学校质量,由联合概率分布表可得:P(A)=0.461,P(B)=0.426,P(A∩B)=0.218。而
P(A)P(B)=0.461×0.426=0.196≠P(A∩B)
因此A与B不是独立的。
34下表显示了正常人群的血型分布(俄亥俄州辛辛那提Hoxworth血液中心提供,2003.3)。
表4-14


解:a.P(O)=0.38+0.06=0.44
b.P(Rh-)=0.06+0.02+0.01+0.06=0.15
c.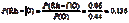
d.P(Rh+)=1-P(Rh-)=1-0.15=0.85

e.假设此对夫妇的血型是相互独立的,则
P(两人血型同为Rh-)=P(Rh-)P(Rh-)=0.15×0.15=0.0225
f.假设此对夫妇的血型是相互独立的,则
P(两人血型同为AB)=P(AB)P(AB)=0.05×0.05=0.0025
35美国劳工统计局收集了年龄在25~65岁之间劳动者的职业分布(Statistical Abstract of the United States,2002),表4-15为各个职业男性和女性的数量(单位:百万)。
表4-15

a.根据上述数据求联合概率分布表。
b.女性从事管理或者专业工作的概率为多少?
c.男性从事精密制造工作的概率为多少?
d.职业与性别是否独立?利用概率值进行解释。
解:a.由表4-15可得联合概率分布表,如表4-16所示。
表4-16 联合概率分布表
| 职业 |
男性 |
女性 |
总计 |
| 管理人员和专业人员 |
0.17 |
0.17 |
0.34 |
| 技术、销售和行政人员 |
0.10 |
0.17 |
0.27 |
| 服务人员 |
0.04 |
0.07 |
0.12 |
| 精密制造人员 |
0.11 |
0.01 |
0.12 |
| 操作、制作人员和劳工 |
0.10 |
0.03 |
0.13 |
| 农、林、渔 |
0.02 |
0.00 |
0.02 |
| 总计 |
0.54 |
0.46 |
1.00 |
b.令MP=管理人员和专业人员,F=女性,则

c.令PP=精密制造人员,M=男性,则

d.由于P(PP|M)=0.20,P(PP)=0.12,P(PP|M) P(PP),所以职业与性别不是独立的。
P(PP),所以职业与性别不是独立的。

解:a.令A=第一次罚球命中,B=第二次罚球命中,则
P(A B)=P(A)P(B)=0.89×0.89=0.7921
B)=P(A)P(B)=0.89×0.89=0.7921
b.至少一次罚球命中的概率为:
P(A B)=P(A)+P(B)-P(A
B)=P(A)+P(B)-P(A B)=0.89×0.89-0.7921=0.9879
B)=0.89×0.89-0.7921=0.9879
c.P(AC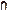 BC)=1-P(A
BC)=1-P(A B)=1-0.9878=0.0121
B)=1-0.9878=0.0121
d.由于印第安纳步行者队的中锋的罚球命中率为58%,即P(A)=0.58。因此
P(A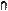 B)=0.58×0.58=0.3364
B)=0.58×0.58=0.3364
P(A B)=0.58+0.58-0.3364=0.8236
B)=0.58+0.58-0.3364=0.8236
P(AC BC)=1-0.8236=0.1764
BC)=1-0.8236=0.1764
雷杰 米勒两次罚球都命中的概率是0.7921,然而中锋两罚均命中的概率仅为0.3364,雷杰
米勒两次罚球都命中的概率是0.7921,然而中锋两罚均命中的概率仅为0.3364,雷杰 米勒两次罚球均未命中的概率是0.0121,而中锋两罚均未命中的概率要高于米勒,为0.1764。因此对手的策略是应对中锋犯规。
米勒两次罚球均未命中的概率是0.0121,而中锋两罚均未命中的概率要高于米勒,为0.1764。因此对手的策略是应对中锋犯规。

解:令C=消费者使用信用卡,B=年龄在18~24岁的消费者,BC=年龄超过24岁的消费者。则可知 ,
,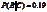 ,
, ,
, 。
。
a.由于 ,所以
,所以
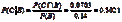
b.由于 ,
, ,因此
,因此
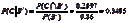
c.年龄在18~24岁的年轻消费者使用信用卡购物的概率较高,其概率为0.5021,而年龄超过24岁的消费者使用信用卡购物的概率仅为0.3485,仅仅大约为年龄在18~24岁的消费者的一半。
d.信用卡公司,如Visa、Maste和Discover都想使利用信用卡购物概率较高的18~24岁的消费者拥有自己公司的信用卡,因此应该允许18~24岁的消费者在建立信用记录之前使用信用卡。公司应对年轻消费者信用额设定的低一些,在他们有能力透支更高的额度时再进行适当的调整。

解:a.P(B)=280/400=0.70
b.喜欢运动饮料的人数=80+40=120,因此P(S)=120/400=0.30
c. =80/120=0.67,
=80/120=0.67,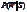 =40/120=0.33
=40/120=0.33
d. =0.30×0.67=0.20;
=0.30×0.67=0.20; =0.30×0.33=0.10
=0.30×0.33=0.10
e.由于P(M)==200/(200+200)=0.50,所以
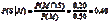
f.由于P(W)=0.50,所以

g.由于 ,
, ,所以某消费者喜欢运动饮料与他是男性或是女性不是相互独立的。
,所以某消费者喜欢运动饮料与他是男性或是女性不是相互独立的。
39A1和A2的先验概率为P(A1)=0.40、P(A2)=0.60,并且已知P(A1∩A2)=0。假设P(B|A1)=0.20且P(B|A2)=0.05。
a.A1和A2是否独立?为什么?
b.计算P(A1∩B)和P(A2∩B)。
c.计算P(B)。
d.利用贝叶斯定理来计算P(A1|B)和P(A2|B)。
解:a.由于P(A1∩A2)=0,所以A1和A2是独立的。
b.P(A1∩B)=P(A1)P(B|A1)=0.40×0.20=0.08
P(A2∩B)=P(A2)P(B|A2)=0.60×0.05=0.03
c.P(B)=P(A1∩B)+P(A2∩B)=0.08+0.03=0.11
d.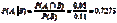

40A1、A2和A3的先验概率为P(A1)=0.20、P(A2)=0.50和P(A3)=0.30,给定A1、A2或A3后事件B的条件概率为P(B|A1)=0.50、P(B|A2)=0.40和P(B|A3)=0.30。
a.计算P(B∩A1)、P(B∩A2)和P(B∩A3)。
b.利用贝叶斯定理——式(4-19)计算后验概率P(A2|B)。
c.利用表格法,根据贝叶斯定理计算P(A1|B)、P(A2|B)和P(A3|B)。
解:a.P(B∩A1)=P(A1)P(B|A1)=0.20×0.50=0.10
P(B∩A2)=P(A2)P(B|A2)=0.50×0.40=0.20
P(B∩A3)=P(A3)P(B|A3)=0.30×0.30=0.09
b.
c.由已知条件可得表4-17。
表4-17
| 事件 |
P(Ai) |
P(B|Ai) |
P(Ai∩B) |
P(Ai|B) |
| A1 |
0.20 |
0.50 |
0.10 |
0.26 |
| A2 |
0.50 |
0.40 |
0.20 |
0.51 |
| A3 |
0.30 |
0.30 |
0.09 |
0.23 |
| 合计 |
1.00 |
— |
0.39 |
1.00 |
41某咨询公司投标一个大型研究项目。该公司管理层起初认为只有一半的可能性中标。然而不久以后,项目的招标委员会要求该公司给出进一步的信息。以往经验表明,75%成功中标的公司和40%投标失败的公司曾被招标委员会要求提供进一步的信息。
a.投标成功的先验概率(即在被要求给出进一步信息之前的中标概率)是多少?
b.若在已知某公司最终会成功中标的前提下,则它被要求提供进一步信息的条件概率是多少?
c.在公司被要求给出进一步信息的前提下,计算投标成功的后验概率。
解:令S1=投标成功,S2=投标未成功,B=要求给出进一步信息。
a.P(S1)=0.50
b.P(B|S1)=0.75
c.
42某地方银行对其信用卡制度进行审核并考虑收回部分信用卡。过去,大约有5%的信用卡持有者不履行债务并造成银行无法收回的坏账。因此,管理层认为某特定的信用卡持有者不履行债务的先验概率为0.05。该银行进一步发现,最终履行债务的信用卡持有者有0.20的概率会拖欠一个或几个月后支付。当然,对于不履行债务的信用卡持有者,拖欠一个或几个月支付的概率为1。
a.如果某个信用卡持有者已经拖欠了一个月的支付,计算他将不履行债务的后验概率。
b.如果某个信用卡持有者不履行债务的概率超过了0.20,银行就将收回他的信用卡。如果某信用卡持有者已经拖欠了一个月的支付,则银行是否会收回他的信用卡?为什么?
解:令M=未按时支付,D1=不履行债务,D2=履行债务。则P(D1)=0.05,P(D2)=0.95,P(M|D2)=0.20,P(M|D1)=1。
a.
b.由于该信用卡持有者将不履行债务的概率为0.21>0.20,所以银行会收回他的信用卡。
43小汽车每英里油耗较少,但不如大汽车安全。小汽车的市场占有率为18%,近年来小汽车事故导致的死亡人数为11898人(Reader‘s Digest,2000.5)。假定事故发生与车型无关,汽车事故中由小汽车发生的概率为0.18,小汽车事故中死亡率为0.128,大汽车事故中死亡率为0.05,则汽车事故中小汽车导致的死亡率为多少?
解:令S=小汽车,Sc=其他类型的汽车,F=汽车事故导致死亡。由题意知,P(S)=0.18,P(Sc)=0.82,P(F|S)=0.128,P(F|Sc)=0.05。利用贝叶斯定理可得表4-18。
表4-18
| 事件 |
先验概率 |
条件概率 |
联合概率 |
后验概率 |
| S |
0.18 |
0.128 |
0.023 |
0.36 |
| Sc |
0.82 |
0.050 |
0.041 |
0.64 |
| 合计 |
1.00 |
— |
0.064 |
1.00 |
由表4-18可知,P(S|F)=0.36,即汽车事故中小汽车导致的死亡率为0.36。

解:a.P(A1)=0.47,P(W|A1)=0.50,P(A2)=0.53,P(W|A2)=0.45。
b.由(a)和贝叶斯定理可得表4-19。
表4-19
| |
先验概率 |
条件概率 |
联合概率 |
后验概率 |
| 事件 |
P(Ai) |
P(W|Ai) |
P(Ai∩W) |
P(Ai|W) |
| 5年内毕业 |
0.47 |
0.50 |
0.2350 |
0.4963 |
| 5年内未毕业 |
0.53 |
0.45 |
0.2385 |
0.5037 |
| |
|
P(W)=0.4735 |
1.0000 |
|
因此P(A1|W)=0.4963,即一名女学生在5年内毕业的概率是0.4963。
c.令M={某学生为男生},则由贝叶斯定理可得表4-20。
表4-20
| |
先验概率 |
条件概率 |
联合概率 |
后验概率 |
| 事件 |
P(Ai) |
P(M|Ai) |
P(Ai∩M) |
P(Ai|M) |
| 5年内毕业 |
0.47 |
0.50 |
0.2350 |
0.4463 |
| 5年内未毕业 |
0.53 |
0.45 |
0.2915 |
0.5537 |
| |
|
P(M)=0.5265 |
1.0000 |
|
因此P(A1|M)=0.4463,即一名男学生在5年内毕业的概率是0.4463。
d.由P(W)=0.4735和P(M)=0.5265可知,大学新生中女生大约占47%,男生大约占53%。
45Money中一篇关于投资增长的文章指出,医药股票表现出强劲的上升趋势,能够为投资者带来稳定和丰厚的收益。联邦卫生保健资金管理部门支持了这个结论,并预测年度处方药消费将由2000年的117亿美元上升至2010年的366亿美元。很多65岁以上的老人严重依赖处方药,82%的老人有规律地服用处方药,其中55%的老人服用三种以上处方药,40%的老人服用5种以上处方药。相反,65岁以下的人中49%的人有规律地服用处方药,其中28%的人服用三种以上处方药,17%的人服用5种以上处方药。由美国人口调查局报告可知,美国现有人口281421906人,其中65岁以上的老人为34991753人。
a.一个美国公民年龄在65岁以上的概率为多少?
b.一个美国公民有规律地服用处方药的概率为多少?
c.一个美国公民65岁以上且有规律地服用5种以上处方药的概率为多少?
d.假定一个美国公民有规律地服用5种以上处方药,他年龄在65岁以上的概率为多少?
解:a.令S=年龄在65岁以上的美国公民。则P(S)= 。
。
b.令D=有规律地服用处方药。则
P(D)=P(D∩S)+P(D∩Sc)=P(D|S)P(S)+P(D|Sc)P(Sc)
=0.82×0.12+0.49×0.88=0.53
c.令D5=服用5种以上处方药,则P(D5∩S)=P(D5|S)P(S)=0.40×0.12=0.048。
d.P(D5)=P(S∩D5)+P(Sc∩D5)=P(D5|S)P(S)+P(D5|Sc)P(Sc)
=0.40×0.12+0.28×0.88=0.048+0.246=0.294
P(S|D5)=
46商业周刊对1035名成人关于商业的态度进行了一次调查(Business Week,2000.9.11)。其中一个问题是:”你如何评价美国大公司的产品质量和全球竞争力”。调查结果:优秀为18%;较好为50%;一般为26%;差为5%;不知道或没回答为1%。
a.随机选取一人,他认为美国大公司表现优秀和较好的概率为多少?
b.认为美国大公司表现差的人数为多少?
c.不知道或没回答的人数为多少?
解:a.P(优秀)=0.18,P(较好)=0.50;P(较好∪优秀)=P(优秀)+P(较好)=0.18+0.50=0.68
b.美国大公司表现差的人数=1035×0.05=52(人)。
c.不知道或没回答的人数=1035×0.01=10(人)。
47某财务经理进行了两项新投资,其中一项投资于石油工业,另一项投资于市政债券。在一年以后,就能够确定这两项投资是否成功。将这两项投资看做一次试验,则
a.在此次试验中共有多少个样本点?
b.绘出树形图并列出样本点。
c.令O=事件”对石油工业的投资成功”,M=”对市政债券的投资成功”。分别列出O和M所包含的样本点。
d.列出两事件的并(O∪M)所包含的样本点。
e.列出两事件的交(O∩M)所包含的样本点。
f.事件O和事件M是否互斥?解释原因。,
解:a.共有2×2=4个样本点。
b.令S=投资成功,U=投资不成功。因此树形图如4-4所示。

图4-4
c.由(b)知,O={E1,E2},M={E1,E3}。
d.O∪M={E1,E2,E3}
e.O∩M={E1}
f.由(e)知,O∩M有一个样本点,所以事件O和事件M不是互斥的。
482003年初,布什总统提议减免股票红利税,他认为在计算公司收入时已经收了税,如果在计算红利时还要收税就是双重收税。关于这一提议对671名美国人进行了调查,发现47%的赞成,44%的人反对,9%的人无所谓。如果从党派来分类,民主党29%的赞成,共和党64%的赞成,无党派人士48%赞成(Investor’s Business Daily,2003.1.13)。
a.有多少人赞成减免税?
b.假定一个被调查者为民主党,则其赞成该提议的概率为多少?
c.党派从属关系与赞成提议事件是否独立?
d.如果假定被调查者的态度都是从自己的利益出发的,那么你认为哪个集团获得的利益最大?
解:a.赞成减免税的人数=0.47×671 315(人)。
315(人)。
b.令F=赞成提议,D=民主党。则P(F|D)=0.29。
c.P(F)=0.47,P(F|D)=0.29
由于P(F)P(F|D),因此党派从属关系与赞成提议事件并不是独立的。
d.因为共和党的赞成比例最高,所以预计共和党获得的利益最大。
49对纽约州的31000例入院治疗的病例进行研究发现,在这些入院治疗的病人中有4%会因为医疗事故而受到伤害。在医疗事故造成的伤害中有1/7导致了死亡。l/4的医疗事故是由于疏忽引起的。每7.5起由疏忽引起的医疗事故中只有1起被承认是工作失误,其中每2起工作失误中仅有l起的病人能得到赔偿。
a.如果某人入院治疗,则他因院方疏忽而遭到医疗事故伤害的概率为多少?
b.如果某人入院治疗,则他会死于医疗事故的概率为多少?
c.如果因疏忽而导致了医疗事故伤害,则病人得到赔偿的概率有多少?
解:令I=因为医疗事故而受到伤害,D=导致死亡,N=疏忽,M=工作失误,$=得到赔偿。由题意可得:P(I)=0.04,P(N|I)=0.25,P(D|I)=1/7,P(M|N)=1/7.5=0.1333,P($|M)=0.50。
a.P(N)=P(N|I)P(I)+P(N|Ic)P(Ic)=0.25×0.04+0×0.96=0.01
b.P(D)=P(D|I)P(I)+P(D|Ic)P(Ic)=1/7×0.04+0×0.96=0.006
c.P(M)=P(M|N)P(N)+P(M|Nc)P(Nc)=0.1333×0.01+0×0.99=0.001333
P($)=P($|M)P(M)+P($|Mc)P(Mc)=0.5×0.001333+0×0.9987=0.00067
50为了了解观众对某一新的电视栏目的反应而进行了一次电话调查,获得的数据如表4-21所示。
表4-21

a.随机选择一名观众,他对新栏目的评价为一般或更好的概率为多少?
b.随机选择一名观众,他对新栏目的评价为一般或更差的概率为多少?
解:a.P(一般或更好)=P(一般)+P(一般以上)+P(很好)
= =0.22+0.28+0.26=0.76
=0.22+0.28+0.26=0.76
b.P(一般或更差)=P(很差)+P(一般以下)=
51表4-22中的数据是2000年美国家庭收入与户主受教育程度的情况(Statistical Abstract of the United States,2002)。
表4-22

a.对上述数据做出联合概率分布表。
b.随机选择一个家庭,户主没有高中毕业的概率是多少?
c.随机选择一个家庭,户主本科毕业或本科以上学历的概率是多少?
d.假定户主本科毕业,其家庭收入在100000美元以上的概率是多少?
e.随机选择一个家庭,其家庭收入低于25000美元的概率是多少?
f.假定户主本科毕业,其家庭收入低于25000美元的概率是多少?
g.家庭收入与户主受教育程度是否独立?
解:a.联合概率分布表如表4-23所示。
表4-23
| 受教育水平 | 家庭收入(千美元) |
合计 | ||||
| 24.9以下 |
25.0-49.9 |
50.0-74.9 |
75.0-99.9 |
100以上 |
||
| 高中以下 |
0.093 |
0.041 |
0.016 |
0.005 |
0.004 |
0.159 |
| 高中毕业 |
0.101 |
0.098 |
0.060 |
0.027 |
0.020 |
0.308 |
| 大专 |
0.060 |
0.082 |
0.058 |
0.032 |
0.031 |
0.264 |
| 本科 |
0.021 |
0.040 |
0.040 |
0.027 |
0.047 |
0.175 |
| 本科以上 |
0.008 |
0.015 |
0.018 |
0.016 |
0.038 |
0.095 |
| 合计 |
0.284 |
0.276 |
0.192 |
0.108 |
0.140 |
1.000 |
b.P(高中以下)=0.093+0.041+0.016+0.005+0.004=0.159
c.P(本科或本科以上)=0.175+0.095=0.27
d.P(100000美元以上|本科)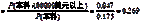
e.P(低于25000美元)=0.284
f.P(低于25000美元|本科)=
g.由于P(低于25000美元)=0.284≠P(低于25000美元|本科),所以家庭收入与户主受教育程度不是独立的。
52毕业生管理委员会(GMAC)对新入学的MBA新生进行调查,表4-24是2018名学生的资料。
表4-24
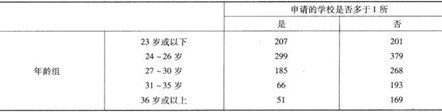
a.随机选择一名MBA新生,对于考察该生的年龄和申请学校数目的试验,做出联合概率分布表。
b.某新生的年龄为23岁或23岁以下的概率为多少?
c.某新生的年龄为26岁或26岁以上的概率为多少?
d.某新生申请学校的数目多于1所的概率为多少?
解:a.由表4-24可得联合概率分布表,如表4-25所示。
表4-25
| |
申请的学校是否多余1所 |
||
| |
是 |
否 |
合计 |
| 23岁或以上 |
0.1026 |
0.0996 |
0.2022 |
| 24~26岁 |
0.1428 |
0.1878 |
0.3360 |
| 27~30岁 |
0.0917 |
0.1328 |
0.2245 |
| 31~35岁 |
0.0327 |
0.0956 |
0.1283 |
| 36岁或以上 |
0.0253 |
0.0837 |
0.1090 |
| 合计 |
0.4005 |
0.5995 |
1.0000 |
b.某新生的年龄为23岁或23岁以下的概率=0.2022。
c.某新生的年龄为26岁或26岁以上的概率=0.2245+0.1283+0.1090=0.4618。
d.某新生申请学校的数目多于1所的概率=0.4005。
53参见上题中MBA新生的调查数据。
a.假定某学生申请学校数目多于l所,则该生年龄在24~26岁的概率为多少?
b.假定某学生在36岁或36岁以上,则该生申请学校的数目多于1所的概率为多少?
c.某学生年龄在24~26岁之间或其申请学校数目多于1所的概率为多少?
d.假设已知某学生只申请了1所学校,则该生年龄在31岁或31岁以上的概率为多少?
e.申请学校的数目和年龄是否独立?试解释原因。
解:a.P(24~26|申请学校数目多于l所)=0.1482/0.4005=0.3700
b.P(申请学校数目多于l所|36岁或以上)=0.0253/0.1090=0.2321
c.P(申请学校数目多于l所或者年龄在24~26)
=0.1026+0.1482+0.1878+0.0917+0.0327+0.0253=0.5883
d.P(31岁或31岁以上|申请了1所学校)=(0.0956+0.0837)/0.5995=0.2991
e.申请学校的数目和年龄并不是独立的,因为条件概率不等于其相应的边际概率,例如P(24~26|申请学校数目多余1所)=0.3700P(24~26)=0.3360。
54IBD/TIPP调查公司对女性和男性投资者进行调查,希望知道他们在决定投资或者撤资时风险因素的影响作用。获得的数据如下,表中的”重要”一词意味着在决定投资或者撤资时风险因素的影响作用大或者很大(Investor’s Business Daily,2000.5.5)。
表4-26

a.受调查者认为在决定投资或者撤资时风险因素的影响重要的概率为多少?
b.男性受调查者认为在决定投资或者撤资时风险因素的影响重要的概率为多少?
c.女性受调查者认为在决定投资或者撤资时风险因素的影响重要的概率为多少?
d.在决定投资或者撤资时,风险因素影响的重要性是否与性别独立?
e.男性与女性对待风险的态度是否不同?
解:令I=风险因素影响是重要的,M=男性,F=女性。
a.P(I)=0.49
b.P(I|M)=0.22/0.50=0.44
c.P(I|F)=0.27/0.50=0.54
d.由于P(I)=0.49P(I|M)=0.44,P(I)=0.49P(I|F)=0.54,所以风险因素影响的重要性与性别是不独立的。
e.由于重视程度取决于性别,所以认为男性和女性受访者对风险有不同的态度。
55一个生产消费品的大型公司为它的某洗涤用品做了电视广告,随后进行了调查。根据调查结果,对下列事件进行概率分配。
B=事件”某人购买了该产品”
S=事件”某人记得看过该产品的广告”
B∩S=事件”某人购买了该产品并且记得看过广告”
概率分配结果为P(B)=0.20、P(S)=0.40,且P(B∩S)=0.12。
a.在某人记得看过该广告的条件下,他购买该产品的概率为多少?广告是否使某人购买该产品的概率增加了?作为决策者,你是否建议继续播出这一广告(假设广告的费用是合理的)?
b.假设不从该公司购买洗涤用品的人都从它的竞争对手那里购买。你估计该公司所占的市场份额有多少?如果继续播出广告,是否会增加该公司的市场份额?为什么?
c.该公司对其另一广告也进行了测验并分配概率为P(S)=0.30且P(B∩S)=0.10。对这则广告,P(B|S)为多少?哪一则广告对消费者有更大的影响?
解:a.
P(B|S)>P(B),即广告使某人购买该产品的概率增加了。
由于该广告增加了购买的概率,所以建议继续播出这一广告。
b.估计该公司所占的市场份额有20%。因为P(B|S)=0.30>P(B)=0.20,所以继续播出广告会增加该公司的市场份额。
c. ,所以第二则广告对消费者影响更大。
,所以第二则广告对消费者影响更大。
56Coorper Realty公司是一家位于纽约州Albany的小型房地产开发公司,主要进行居民住宅的销售。最近,这家公司希望知道在特定的一段时间内一座居民住宅被售出的可能性。通过对去年该公司售出的800座住宅的分析。得到了以下的数据。
表4-27
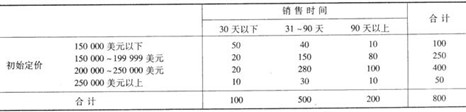
a.定义事件A为”某住宅售出时间超过90天”,估计事件A的概率。
b.定义事件B为”某住宅定价低于150000美元”,估计事件B的概率。
c.事件A∩B的概率为多少?
d.假设某住宅的定价少于150000美元,则该公司需要超过90天的时间才能将其售出的概率为多少?
e.事件A和事件B是否独立?
解:a.P(A)=200/800=0.25
b.P(B)=100/800=0.125
c.P(A∩B)=10/800=0.0125
d.P(A|B)=P(A∩B)/P(B)=0.0125/0.125=0.10
e.由于P(A|B)P(A)=0.25,所以事件A和事件B不是独立的。
57某公司对它设在得克萨斯州Brownsville的一个工厂的误工事件进行了研究。历史记录表明,去年有6%的员工发生过误工事件。管理人员确信,某项特殊的保障措施将会把今年的误工事件减少到5%。此外,据估计在去年发生误工事件的员工中有15%的人今年还会发生此类事件。
a.有百分之多少的员工会在去年和今年都发生误工事件?
b.有百分之多少的员工会在去年和今年两年中至少发生过一次误工事件?
解:令A=今年发生误工事件,B=去年发生误工事件。P(B)=0.06,P(A)=0.05,P(A|B)=0.15。
a.P(A∩B)=P(A|B)P(B)=0.15×0.06=0.009
b.P(A∪B)=P(A)+P(B)-P(A∩B)=0.06+0.05-0.009=0.101
58达拉斯的IRS审计人员正在关注如何确定可能的退税诈骗行为。从过去的经验中他们发现,如果一项退税项目中包含的特别税折扣超过了IRS标准,则存在退税诈骗行为的概率为0.20;如果一项退税项目中包含的特别税折扣未超过IRS标准,则存在退税诈骗行为的概率降为0.02。假设共有8%的特别税折扣超过了IRS标准,则估计退税诈骗行为的百分比为多少?
解:令A=退税诈骗行为,B=退税项目中包含的特别税折扣超过了IRS标准。
由题意知P(A|B)=0.20,P(A|Bc)=0.02,P(B)=0.08,,P(Bc)=1-P(B)=0.92。
P(A)=P(A∩B)+P(A∩Bc)=P(B)P(A|B)+P(Bc)P(A|Bc)
=0.08×0.20+0.92×0.02=0.0344
即估计退税诈骗行为的百分比为3.44%。
59某石油公司购买了一块位于阿拉斯加的土地的开采权。初步的地质研究表明有以下的先验概率。
P(含高质量石油)=0.50
P(含中等质量石油)=0.20
P(不含石油)=0.30
a.发现含有石油的概率为多少?
b.在第一口井钻至200英尺深时,进行了土质检测。在检测中发现的特殊土质类型的概率为下:
P(该土质类型|含高质量石油)=0.20
P(该土质类型|含中等质量石油)=0.80
P(该土质类型|不含石油)=0.10
该公司将如何理解土质检测的结果?发现石油的修正概率,即新的概率是多少?
解:a.P(含有石油)=P(含高质量石油)+P(含中等质量石油)=0.50+0.20=0.70
b.令S=土质检测结果。则由贝叶斯定理可得表4-28。
表4-28
| Events |
P(Ai) |
P(S|Ai) |
P(Ai∩S) |
P(Ai|S) |
| 含高质量石油(A1) |
0.50 |
0.20 |
0.10 |
0.345 |
| 含中等质量石油(A2) |
0.20 |
0.80 |
0.16 |
0.552 |
| 不含石油(A3) |
0.30 |
0.10 |
0.03 |
0.103 |
| 合计 |
1.00 |
P(S)=0.29 |
1.00 |
|
经过土质检测,发现石油的概率较高,但是该块土地含有中等质量石油的概率大于含有高质量石油的概率。发现石油的修正概率,即新的概率是0.897(0.345+0.552)。
60公司在从事互联网业务时总能通过先前被访问的网址来获取网络访问者的概率分布信息。在一篇《网络市场》的文章中(Interfaces 2001.3.4),描述了如何通过点击率和贝叶斯定理来确定网络访问者的性别。Par Fore建立了一个销售高尔夫用品的网站,并希望对女性访问者和男性访问者分别提供不同的价格。从过去互联网访问者的抽样可知,Par Fore.com网站的访问者中60%为男性,40%为女性。
a.下一个访问者为女性的先验概率为多少?
b.假设一个访问者先前访问过Dillard网站,而这个网站的女性访问者数量是男性的三倍。试问,该如何修正下一个访问者为女性的概率?此刻你该报出针对女性访问者的价格还是针对男性访问者的价格?
解:a.令F=女性,则下一个访问者为女性的先验概率P(F)=0.40。
b.令D=Dillard网站。由于Dillard网站的女性访问者数量是男性的三倍,即P(F)= ,则下一个访问者为女性的修正概率为:
,则下一个访问者为女性的修正概率为:

由于其修正概率大于0.5,所以此刻应报出针对女性访问者的价格。
