云南大学432统计学考研真题及辅导用书

考研真题

1. 云南大学数学与统计学院《432统计学》[专业硕士]历年考研真题

2. 全国名校应用统计硕士《432统计学》考研真题精选

3. 应用统计硕士《432统计学》名校考研真题（2017年前）

考研指导书

1. 袁卫《统计学》（第5版）配套题库【考研真题精选＋课后习题＋章节题库】

2. 浙江大学《概率论与数理统计》（第5版）配套题库【考研真题精选＋章节题库】

云南大学数学与统计学院《432统计学》[专业硕士]历年考研真题AI讲解

书籍目录

部分内容

2011年云南大学数学与统计学院432统计学[专业硕士]考研真题

2011年云南大学数学与统计学院432统计学[专业硕士]考研真题详解

一、单项选择题

1

【答案】D

【解析】抽样调查是一种非全面调查，它是按照随机原则从总体中抽取一部分单位作为样本进行观察研究，以抽样样本的指标去推算总体指标的一种调查。随机原则要求所有调查单位都有一定的概率被抽取。

2

【答案】A

【解析】测度集中趋势的指标通常为众数、中位数、分位数和均值；测度离散趋势的指标通常有极差、内距、方差和标准差以及离散系数。均值反映了总体分布的集中趋势。

3

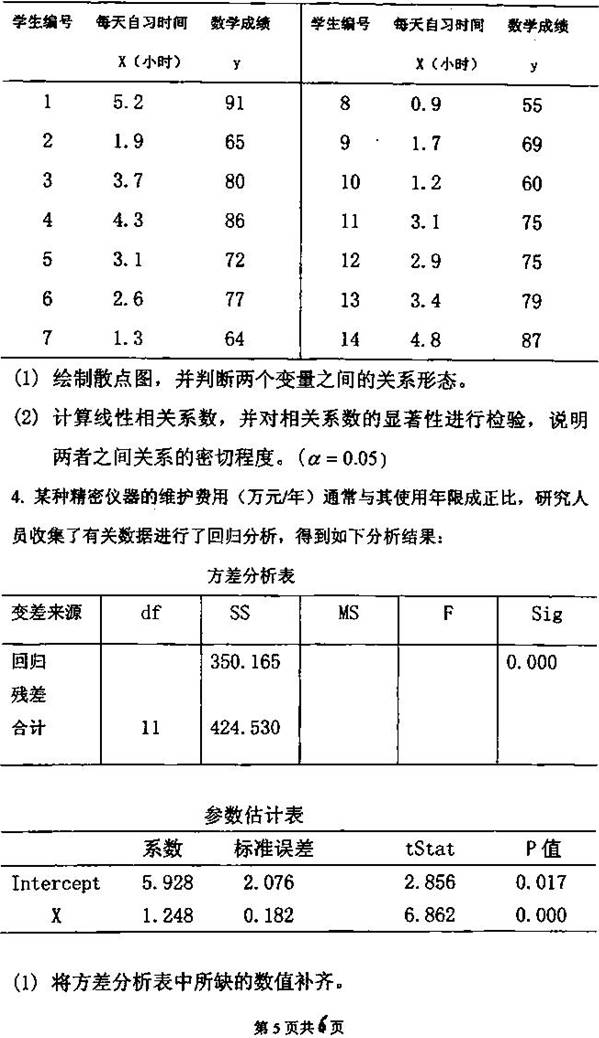
【答案】B

【解析】设总体均值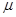为，标准差为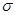，样本容量为n。根据中心极限定理，当n充分大时，样本均值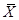的抽样分布近似服从均值为μ、方差为σ²/n的正态分布。因此有：

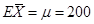
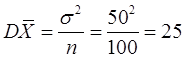
4

【答案】B

【解析】简单算术平均值的计算公式为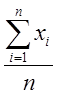，其中n为变量个数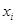，为变量的具体数值，可以看成每个变量值的权重均为1，即它不受权数大小的影响。x­i越大，随着变量个数的增加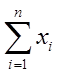也会随之增加，因此影响简单算术平均值的是变量值的大小而不是变量的个数。

5

【答案】D

【解析】设A₁表示事件“甲种产品畅销”，A₂表示事件“乙种产品滞销”，则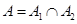，故

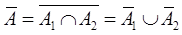
即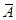表示事件“甲种产品滞销或乙种产品畅销”。

6

【答案】C

【解析】

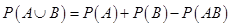
由于A与B相互独立，有P（AB）＝P（A）P（B），因此

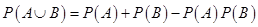
即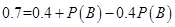，解得。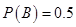

7

【答案】A

【解析】“至少有一个黑球”的对立事件为“3个球全是白球”，故至少有一个黑球的概率为

8

【答案】C

【解析】对置信水平为95%的置信区间的理解为：如果用某种方法构造的所有区间中有95%的区间包含总体参数的真值，5%的区间不包含总体参数的真值，那么用该方法构造的区间称为置信水平为95%的置信区间。当实验次数趋于无穷大时，可以理解为某区间以95%的概率包含参数值。参数值是一个定值，要么在一个区间内，要么不在这个区间内，不存在以多大可能性落入某一区间这种说法。

9

【答案】D

【解析】总体比例区间估计的允许误差为

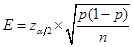
将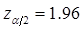，代入计算得：

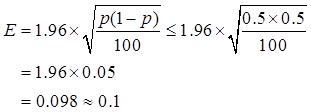
10

【答案】B

【解析】总体分布为正态分布且方差已知时用Z分布构造置信区间；总体分布不是正态分布，但在大样本情况下近似服从正态；总体分布未知，方差已知应采用非参数估计；总体分布服从正态分布且方差未知时用t分布构造置信区间。

11

【答案】B

【解析】在假设检验中一般是把希望证明的命题放在备择假设上，而把原有的、传统的观点或结论放在原假设上，本题中营养不良人数的比率高达20%是原有的结论，是需要推翻的，应该放在原假设上；营养不良人数的比率比20%还要高是需要证明的结论，应该放在备择假设上。

12

【答案】A

【解析】当显著性水平为0.01时拒绝原假设，说明P值小于0.01，因此P值也小于0.05，故α＝0.05时一定会拒绝原假设。

13

【答案】B

【解析】一元线性回归方程的形式为：E（y）＝β₀＋β₁x。其中β₁是直线的斜率，它表示当x每变动一个单位时，y的平均变动值。题中，回归方程的回归系数为b，表示自变量每变动一个单位时，因变量平均变动b个单位。

14

【答案】B

【解析】在多元线性回归分析中，t检验是用来检验各个回归系数是否显著，F检验是用来检验回归方程是否显著。

15

抱歉，本题不提供答案！

二、简答题

1

答：由部分来推断总体，判断有可能正确，也有可能不正确，即有犯错误的可能。所犯的错误有两种类型，第I类错误是原假设H₀为真却被拒绝了，犯这种错误的概率用α表示，所以也称α错误或拒真错误；第II类错误是原假设为伪却没有被拒绝，犯这种错误的概率用β表示，所以也称β错误或采伪错误。

对于一定的样本量n，如果减小α错误，就会增大犯β错误的机会；若减小β错误，也会增大犯α错误的机会。要使α和β同时变小，只有增大样本量。

2

答：相关系数的取值区间为[－1，1]，若0＜r≤1，表明变量x与y之间存在正线性相关关系；若－1≤r＜0，表明x与y之间存在负线性相关关系；当相关系数为1时，两变量之间完全正相关；当相关系数为－1时，两变量之间完全负相关；其绝对值越接近1，说明线性相关关系越强，当相关系数为0时，两变量之间不存在线性关系。

3

答：统计学中评价估计量好坏的标准通常为无偏性、相合性和有效性。

（1）无偏性

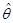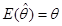无偏性是指估计量抽样分布的数学期望等于被估计的总体参数。设总体参数为θ，所选择的估计量为，如果，则称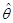为θ的无偏估计量。

（2）有效性

有效性是指对同一总体参数的两个无偏估计量，有更小标准差的估计量更有效。

（3）相合性

相合性是指随着样本量的增大，估计量的值越来越接近被估总体的参数。换言之，一个大样本给出的估计量要比一个小样本给出的估计量更接近总体的参数。

4

答：在回归模型中，因变量y的取值是不同的，y取值的这种波动称为变差。变差的产生来自两个方面：①由自变量x的取值不同造成的；②除x以外的其他因素（如x对y的非线性影响、测量误差等）的影响。

（1）总平方和（SST）

对一个具体的观测值来说，变差的大小可以用实际观测值y与其均值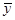之差来表示。而行次观测值的总变差可由这些离差的平方和来表示，称为总平方和，记为SST；

（2）回归平方和（SSR）

把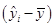看做由于自变量x的变化引起的y的变化，而其平方和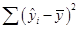则反映了y的总变差中由于x与y之间的线性关系引起的y的变化部分，它是可以由回归直线来解释的y_i的变差部分，称为回归平方和，记为SSR；

（3）残差平方和（SSE）

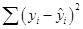是各实际观测点与回归值的残差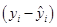平方和，它是除了x对y的线性影响之外的其他因素引起的y的变化部分，是不能由回归直线来解释的y_i的变差部分，称为残差平方和或误差平方和，记为SSE。

三个平方和的关系为：总平方和（SST）＝回归平方和（SSR）＋残差平方和（SSE）。

三、计算题

1

解：由于n＝31＞30，所以该样本为大样本。在大样本条件下，样本均值近似服从正态分布，因此检验统计量为

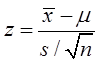
在95%的置信水平下，总体均值的区间估计为

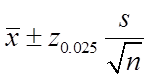
代入数据计算得该家庭每天平均电费的置信区间为

2

解：该检验的原假设与备择假设分别为

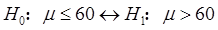
检验的统计量为

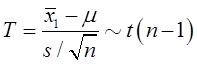
由数据算得

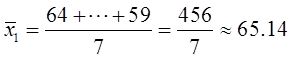
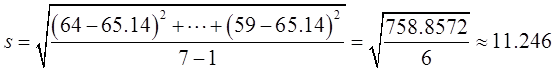
代入检验统计量的公式中得

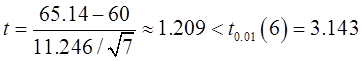
因此不能拒绝原假设，即促销无效。

3

解：（1）散点图如下所示：

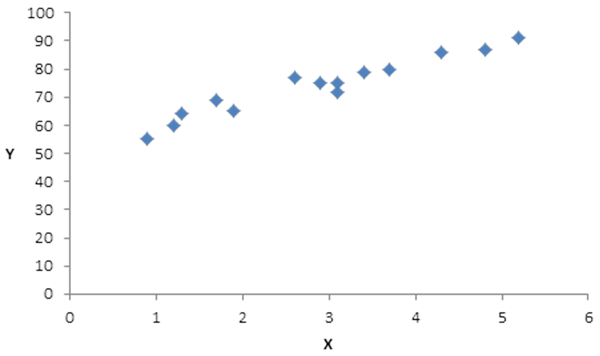
由图可看出，X和Y大致上呈正线性关系，随着X的增加Y也线性增加。

（2）设相关系数为r，其计算公式为

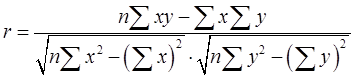
其中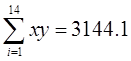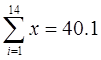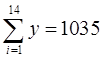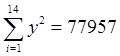，，，，，n＝14，代入计算得到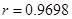。说明每天学习时间和数学成绩高度正相关。

相关系数的显著性检验：原假设和备择假设分别为H₀：ρ＝0；H₁：ρ≠0，检验的统计量为

检验的拒绝域为|t|＞t_a/2（n－2）。代入数据计算得t＝13.7738＞2.179，因此拒绝原假设，即相关系数显著不为0。

通过相关系数的计算及其显著性检验，说明每天的自习时间和数学成绩有非常显著的线性相关关系，且呈现高度正相关。

4

解：（1）由于自变量仅使用年限这一个变量，因此回归的自由度为1；由于总的自由度为11，故残差的自由度为11－1＝10；残差平方和＝总平方和－回归平方和＝424.530－350.165＝74.365；回归的均方误差为350.165/1＝350.165，残差的均方误差为74.365/10＝7.4365；因此F＝350.165/7.4365＝47.087。根据计算结果补齐方差分析表如下：

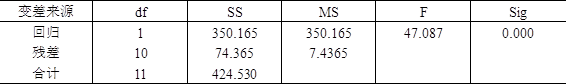
（2）

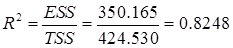
因此维护费用的变差中有82.48%可由使用年限解释。

（3）根据参数估计表，可知回归方程为

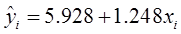
回归系数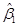表示使用年限每增加一年，维护费用平均增长1.248万元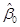；无实际意义，仅是回归方程的截距项。

更多内容，请点击获取：
http://shuyue.100xuexi.com/Ebook/978028.html