考研真题
1. 西南大学数学与统计学院《432统计学》[专业硕士]历年考研真题
2. 全国名校应用统计硕士《432统计学》考研真题精选
3. 应用统计硕士《432统计学》名校考研真题(2017年前)
考研指导书
1. 2026年应用统计硕士《432统计学》专用教材
2. 2026年应用统计硕士《432统计学》考研题库

西南大学数学与统计学院《432统计学》[专业硕士]历年考研真题AI讲解
书籍目录
2012年西南大学数学与统计学院432统计学[专业硕士]考研真题
2012年西南大学数学与统计学院432统计学[专业硕士]考研真题及详解
2011年西南大学数学与统计学院432统计学[专业硕士]考研真题(部分)
2011年西南大学数学与统计学院432统计学[专业硕士]考研真题(部分)及详解

部分内容
2012年西南大学数学与统计学院432统计学[专业硕士]考研真题






2012年西南大学数学与统计学院432统计学[专业硕士]考研真题及详解
参考答案
西南大学
2012年攻读硕士学位研究生入学考试试题
学科、专业:应用统计 研究方向:各方向
试题名称:统计学 试题编号:432
(答题一律做在答题纸上,并注明题目番号,否则答题无效)
一、单项选择题(8小题,每小题5分,共40分)
1设事件A、B相互独立,且P(A)=0.1,P(B)=0.4,则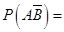 (
(
).
(A)0.04,
(B)0.06,
(C)0.36,
(D)0.42,
【答案】B
【解析】事件A、B相互独立,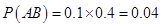
则有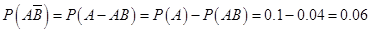
2将三个球随机地放入4个杯子中去,杯子中球的最大个数是l的概率为( ).
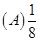
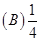
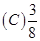
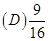
【答案】C
【解析】杯子中球的最大个数是l,说明有一个杯子是空的,其他三个杯子各有一个球。三个球随机地放入4个杯子中去有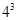 种放法,结果为杯子中球的最大个数是l有
种放法,结果为杯子中球的最大个数是l有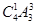 种放法。则这种结果的概率
种放法。则这种结果的概率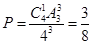 .
.
3以X表示某商店从早晨开始营业起直到第一顾客到达的等待时间(以分计),X的分布函数是
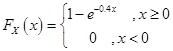
,则等待时间恰好3分钟的概率为( ).
(A)0,
(B)e-1.2,
(C)1-e-1.2,
(D)1.
【答案】C
【解析】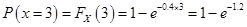
4将n只球(1~n号)随机地放进n只盒子(1~n号)中去,一只盒子装一只球。将一只
球装入与球同号的盒子中,称为一个配对,记X为配对的个数,则E(X)=(
).
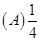
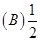
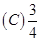
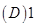
【答案】D
【解析】记事件 ,每个盒子独立看能够配对的概率是
,每个盒子独立看能够配对的概率是
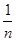 ,则有
,则有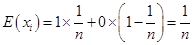 ,得
,得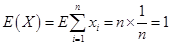
5设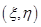 为二维随机变量,且
为二维随机变量,且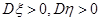 则下列等式成立的是(
则下列等式成立的是(
).
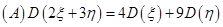
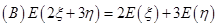
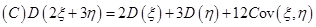
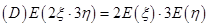
【答案】B
【解析】二维随机变量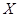 ,
,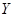 的期望和方差具有以下几个性质:
的期望和方差具有以下几个性质:
①设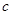 是常数,则
是常数,则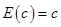 ,
,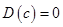 ;
;
②设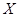 是随机变量,
是随机变量,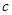 是常量,则有
是常量,则有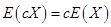 ,
,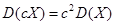 ;
;
③设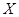 ,
,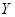 是随机变量,则有
是随机变量,则有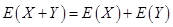 ,
,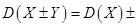
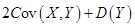
;
④设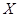 ,
,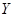 是两个不相关的随机变量,则
是两个不相关的随机变量,则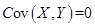 ,
,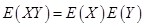 ,
,
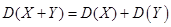
。
由性质2和3可得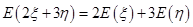 。
。
6设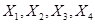 是总体
是总体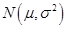 的样本,
的样本,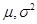 未知,则统计量是(
未知,则统计量是(
).
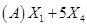
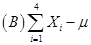
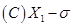
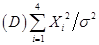
【答案】A
【解析】设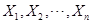 是从总体
是从总体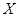 中抽取的容量为
中抽取的容量为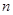 的一个样本,如果由此样本构造一个函数
的一个样本,如果由此样本构造一个函数
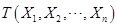 ,不依赖于任何未知参数,则称函数
,不依赖于任何未知参数,则称函数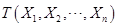 是一个统计量。由此可知统计量是不含未知参数的样本函数,根据定义可知BCD三项都含未知参数
是一个统计量。由此可知统计量是不含未知参数的样本函数,根据定义可知BCD三项都含未知参数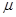 或
或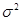 ,所以都不是统计量。
,所以都不是统计量。
7设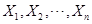 来自总体
来自总体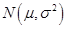 ,且相互独立,则随机变量
,且相互独立,则随机变量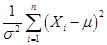 服从的分布是(
服从的分布是(
).
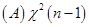
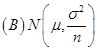
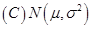
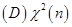
【答案】D
【解析】设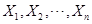 是来自总体
是来自总体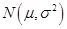 的样本,则有
的样本,则有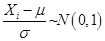 ,
,
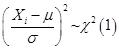 ,
,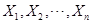 是相互独立的,则随机变量
是相互独立的,则随机变量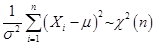
8设总体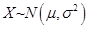 ,
,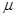 未知,
未知,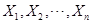 为样本,S2为修正样本方差,则检验
为样本,S2为修正样本方差,则检验
问题: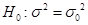 ,
,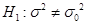 (
(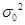 已知)的检验统计量为( ).
已知)的检验统计量为( ).
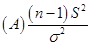
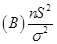
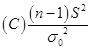
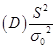
【答案】C
【解析】由于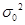 已知,故方差检验所使用的是
已知,故方差检验所使用的是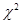 统计量,这是因为
统计量,这是因为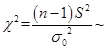
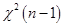 ,其中
,其中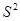 是指修正后的样本方差,是
是指修正后的样本方差,是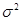 的无偏估计,本题中进行的是双侧检验。
的无偏估计,本题中进行的是双侧检验。
二、填空题(6小题,每小题5分,共30分)
1从5双不同鞋子中任取4只,4只鞋子中至少有2只配成一双的概率是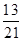 。
。
【解析】从五双不同鞋子中任取4只有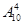 种取法。4只鞋子中没有配成一双有
种取法。4只鞋子中没有配成一双有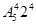 种取法,则4只鞋子中至少有两只配成一双的概率是P=
种取法,则4只鞋子中至少有两只配成一双的概率是P=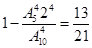 。
。
2设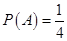 ,
,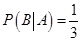 ,
,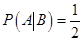 ,则
,则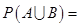
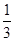
【解析】因为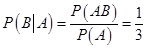 ,则
,则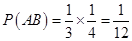 ,又已知
,又已知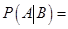
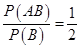 ,则
,则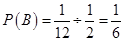 ,而
,而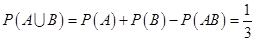 .
.
3设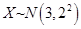 ,则
,则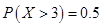 .
.
【解析】在连续性随机变量中某一点处的概率为0,即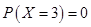 ,
,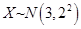 可知该正态分布关于
可知该正态分布关于
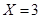 中心对称,则有
中心对称,则有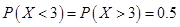
4对敌人防御地段进行l00次轰炸,每次命中目标的炸弹数是一个随机变量,其期望值是2,方差是l.69,则l00次轰炸中有187~213颗命中目标的概率0.6826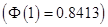
【解析】设第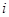 次轰炸命中目标的炸弹数为
次轰炸命中目标的炸弹数为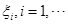 则100次轰炸命中目标的炸弹数
则100次轰炸命中目标的炸弹数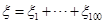 ,且
,且
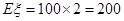 ,
,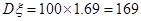 ,由中心极限定理可知,
,由中心极限定理可知,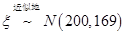 ,则有
,则有
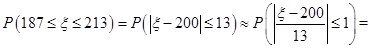
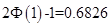
5设总体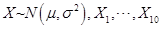 是来自X的样本。则
是来自X的样本。则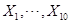 的联合概率密度为
的联合概率密度为
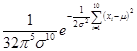
。
【解析】由于总体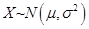 ,则连续型随机变量
,则连续型随机变量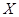 的概率密度为:
的概率密度为:
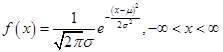
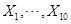 是来自
是来自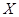 的样本,所以它们相互独立且同分布,则
的样本,所以它们相互独立且同分布,则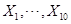 的联合概率密度
的联合概率密度
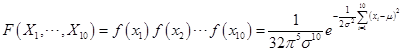
6设样本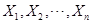 来自总体
来自总体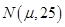 ,则
,则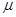 的置信度为
的置信度为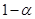 的置信区间为
的置信区间为
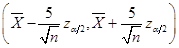
.
【解析】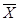 是
是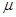 的无偏估计,且有
的无偏估计,且有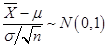 ,则
,则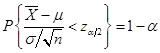 ,即
,即
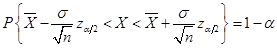 ,则
,则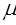 的置信度为
的置信度为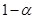 的置信区间为:
的置信区间为:
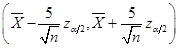
。
三、简述题(共4小题,每小题5分,共20分)
1给出简单随机样本的概念。
答:
设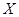 是具有分布函数
是具有分布函数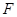 的随机变量,若
的随机变量,若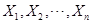 是具有同一分布函数
是具有同一分布函数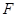 的、相互独立的随机变量,则称
的、相互独立的随机变量,则称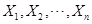 为从分布函数
为从分布函数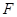 (或总体
(或总体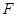 、或总体
、或总体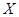 )得到的容量为
)得到的容量为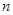 的简单随机样本,简称样本。它们的观察值
的简单随机样本,简称样本。它们的观察值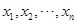 称为样本值,又称为
称为样本值,又称为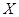 的
的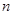 个独立的观察值。
个独立的观察值。
简单随机样本的两个主要特点是①随机变量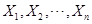 之间是相互独立的;②随机变量
之间是相互独立的;②随机变量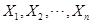 服从同样的分布,即有相同的概率密度函数(分布函数)。
服从同样的分布,即有相同的概率密度函数(分布函数)。
2简述矩估计的一般步骤。
答:用样本矩作为总体矩的估计量,用样本矩的连续函数作为总体矩的连续函数的估计量,这种估计方法叫做矩估计法。
矩估计的一般步骤:
(1)设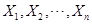 是总体
是总体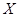 的简单随机样本,已知
的简单随机样本,已知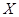 的分布函数
的分布函数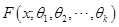
其中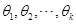 是待估参数。
是待估参数。
(2)设总体的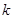 阶原点矩为
阶原点矩为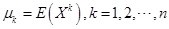 存在,则样本的
存在,则样本的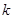 阶矩由大数定律可知,
阶矩由大数定律可知,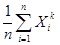 以概率收敛到
以概率收敛到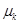 ,即用
,即用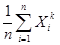 估计
估计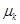 ,令
,令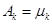 ,由此得到一个包含
,由此得到一个包含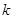 个未知参数
个未知参数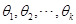 的联立方程组。从中解得
的联立方程组。从中解得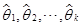 即为矩估计量。矩估计量的观察值称为矩估计值。
即为矩估计量。矩估计量的观察值称为矩估计值。
3点估计的评价标准有哪些?
答:点估计的评价标准有:无偏性、有效性、相合性(一致性)、均方误差。
(1)无偏性
设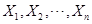 是总体
是总体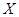 的一个样本,
的一个样本,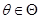 是包含在总体
是包含在总体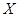 的分布中的待估参数,这里
的分布中的待估参数,这里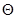 是
是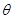 的取值范围。若估计量
的取值范围。若估计量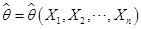 的数学期望
的数学期望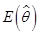 存在,且对于任意
存在,且对于任意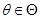 有
有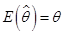 ,则称
,则称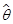 是
是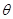 的无偏估计量。
的无偏估计量。
(2)有效性
设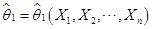 与
与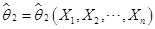 都是
都是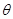 的无偏估计量,若对于任意
的无偏估计量,若对于任意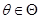 ,有
,有
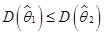 且至少对于某一个
且至少对于某一个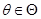 上式中的不等号成立,则称
上式中的不等号成立,则称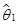 较
较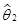 有效。
有效。
(3)相合性(一致性)
设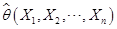 为参数
为参数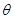 的估计量,若对于任意
的估计量,若对于任意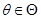 ,当
,当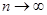 时
时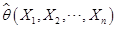 以概率收敛于
以概率收敛于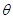 ,则称
,则称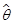 为
为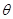 的相合估计量。即,若对于任意
的相合估计量。即,若对于任意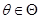 都满足:对于任意
都满足:对于任意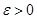 ,有
,有
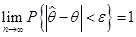
则称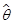 是
是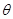 的相合估计量。
的相合估计量。
关于一致性的两个常用结论:
①样本K阶矩是总体K阶矩的一致估计量。
②若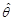 是
是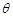 的无偏估计量,并且
的无偏估计量,并且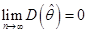 ,则
,则
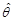 是
是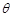 的一致估计量。
的一致估计量。
(4)均方误差
设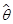 是
是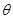 的一个估计(有偏的或无偏的),则称
的一个估计(有偏的或无偏的),则称
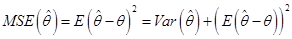
为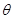 的均方误差。均方误差较小意味着:
的均方误差。均方误差较小意味着: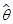 不仅方差较小,而且偏差
不仅方差较小,而且偏差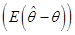 也小,所以均方误差是评价点估计的最一般的标准。
也小,所以均方误差是评价点估计的最一般的标准。
4构造置信区间的枢轴量法的具体步骤是什么?
答:构造置信区间的枢轴量法的具体步骤:
(1)从未知参数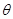 的某个点估计
的某个点估计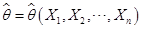 出发,构造
出发,构造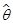 与
与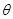 的一个函数
的一个函数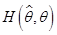 使得
使得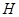 的分布(在大样本场合,可以是
的分布(在大样本场合,可以是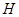 的渐近分布)已知,且与
的渐近分布)已知,且与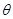 无关。该函数通常称为枢轴量。
无关。该函数通常称为枢轴量。
(2)适当选取两个常数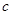 与
与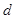 ,使对给定的
,使对给定的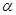 有
有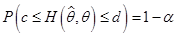 .
.
(3)利用不等式运算,将不等式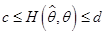 进行等价变形,使得最后能得到形如
进行等价变形,使得最后能得到形如
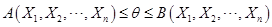
的不等式。即
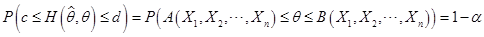
此时参数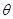 的置信度为
的置信度为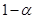 的置信区间为
的置信区间为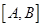 。
。
四、解答题(共5小题,每小题10分,共50分)
1已知男人中有5%是色盲患者,女人中有0.25%是色盲患者。今从男女人数相等的人群中随机地挑选一人,恰好是色盲患者,问此人是男性的概率是多少?
解:记事件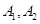 分别表示从男女人数相等的人群中随机地挑选一人为男性、女性,事件
分别表示从男女人数相等的人群中随机地挑选一人为男性、女性,事件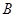 为色盲者,则有
为色盲者,则有
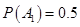 ,
,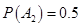
利用全概率公式可得:
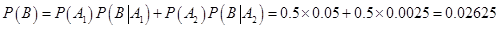
利用贝叶斯公式可得:
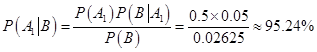
则明此人是男性的概率是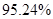 。
。
2设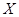 在
在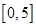 上服从均匀分布,试求方程
上服从均匀分布,试求方程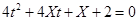 有实根的概率。
有实根的概率。
解:方程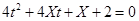 有实根的充要条件是
有实根的充要条件是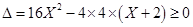 ,解得
,解得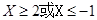 ,根据已知条件
,根据已知条件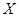 在
在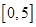 上服从均匀分布,可知
上服从均匀分布,可知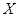 的密度函数为:
的密度函数为:
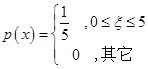
可得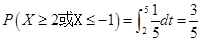 ,说明方程
,说明方程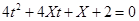 有实根的概率为
有实根的概率为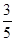 。
。
3设二维随机变量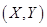 的概率密度为
的概率密度为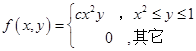
(1)试确定常数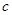 .
.
解:
(1)
由于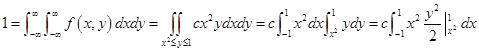
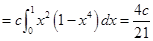
得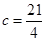 。
。
(2)求边缘概率密度.
解: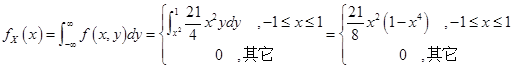
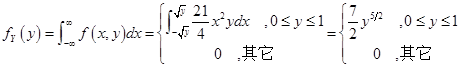
4设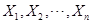 是总体
是总体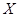 的一个样本,
的一个样本,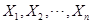 为一相应的样本值。总体X的概率密度函数为
为一相应的样本值。总体X的概率密度函数为
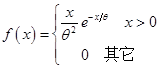 ,
,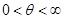 ,求参数
,求参数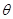 的最大似然估计量和估计值。
的最大似然估计量和估计值。
解:构造似然函数: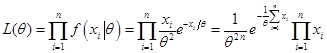
对数似然函数: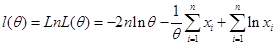
令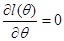 ,则
,则
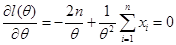
,
得到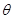 的最大似然估计值为
的最大似然估计值为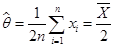
相应的最大似然估计量为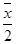 。
。
五、证明题(10分)
设随机变量X和Y的联合分布为:
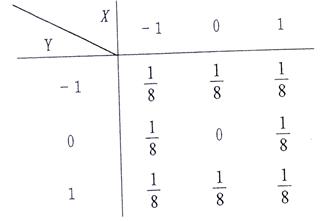
试证明X和Y不相关,但X和Y不相互独立的。
解: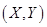 为二维随机变量,
为二维随机变量,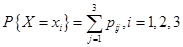 ,
,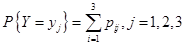
根据随机变量X和Y的联合分布表得:
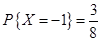 ,
,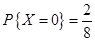 ,
,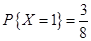
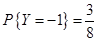 ,
,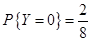 ,
,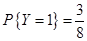
则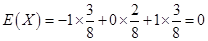 ,
,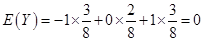
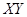
的联合分布为:
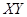
|
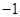
|

|
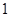
|
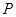
|
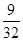
|
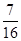
|
 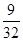
|
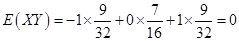 ,即有
,即有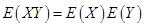 ,说明
,说明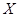 与
与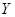 不相关。
不相关。
X与Y是不相关的,但是不一定是独立的,即独立是不相关的充分非必要条件。要证明X与Y是非独立的用反证法,举反例即可。
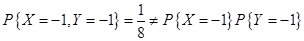 ,
,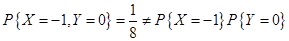
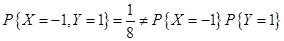
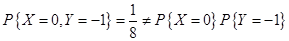
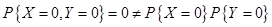
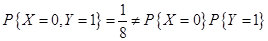
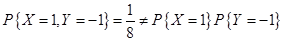
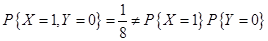
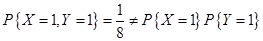
由此可知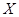 和
和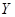 是不相互独立的。
是不相互独立的。
更多内容,请点击获取:
http://shuyue.100xuexi.com/Ebook/973705.html
