考研真题
1. 全国名校概率论与数理统计考研真题汇总（含部分答案）
考研指导书
1. 茆诗松《概率论与数理统计教程》（第3版）笔记和课后习题（含考研真题）详解
2. 茆诗松《概率论与数理统计教程》（第3版）配套题库【考研真题精选＋章节题库】
3. 浙江大学《概率论与数理统计》（第5版）配套题库【考研真题精选＋章节题库】
茆诗松《概率论与数理统计教程》（第3版）笔记和课后习题（含考研真题）详解
书籍目录
第1章 随机事件与概率
第2章 随机变量及其分布
第3章 多维随机变量及其分布
第4章 大数定律与中心极限定理
第5章 统计量及其分布
第6章 参数估计
第7章 假设检验
第8章 方差分析与回归分析
部分内容
第1章 随机事件与概率
1.1 复习笔记
一、随机事件及其运算
1事件间的运算（见表1-1-1）
表1-1-1 事件间的运算
注：①对立事件是相互的。必然事件与不可能事件互为对立事件。
②A与B互为对立事件⇔A∩B＝∅，且A∪B＝Ω。
③对立事件一定是互不相容的事件，反之不一定。
④A－B⇔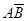
。
2事件的运算性质（见表1-1-2）
表1-1-2 事件的运算性质
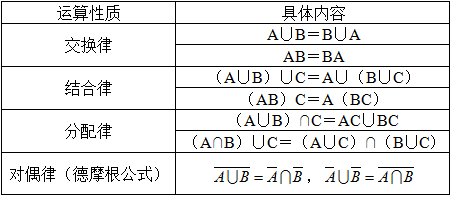
二、概率的定义及其确定方法
确定概率的频率方法
（1）确定概率的频率方法
∫n（A）＝事件A的频数/n
（2）确定概率的古典方法
P（A）＝事件所包含样本点的个数/Ω中所有样本点的个数＝k/n。
（3）确定概率的几何方法
P（A）＝SA/SD
三、概率的性质
1概率的可加性
（1）若有限个事件A1，A2，…An互不相容，则
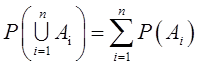
（2）对任一事件A，有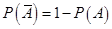
。
2概率的单调性
（1）（单调性）若A⊃B，则P（A）≥P（B）反之不成立。
（2）任意事件A，B，P（A－B）＝P（A）－P（AB）。
3概率的加法公式
（1）（加法公式）对任意两个事件A，B，有
P（A∪B）＝P（A）＋P（B）－P（AB）
对任意n个事件A1，A2，…，An，有
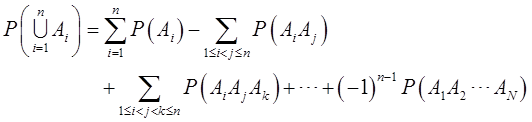
（2）（半可加性）对任意两个事件A，B，有
P（A∪B）≤P（A）＋P（B）
对任意n个事件A1，A2，…An，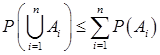
。
四、条件概率
1条件概率的定义
P（A|B）＝P（AB）/P（B）
2三个非常实用的公式
（1）乘法公式
①若P（B）＞0，则P（AB）＝P（B）P（A|B）；
②若P（A1A2…An－1）＞0，则P（A1A2…An）＝P（A1）P（A2|A1）P（A3|A1A2）…P（An|A1…An－1）；
（2）全概率公式
设B1，B2，…Bn为样本空间的一个分割，即B1，B2，…Bn互不相容，且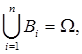
如果P（Bi）＞0，i＝1，2，…，n，则对任一事件A有
。
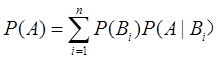（3）贝叶斯公式
设B1，B2，…Bn是样本空间Ω的一个分割，即B1，B2，…Bn互不相容，且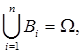
如果P（A）＞0，P（Bi）＞0，i＝1，2，…n，则
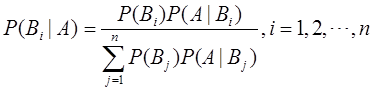
五、独立性
1两个事件的独立性
P（AB）＝P（A）P（B）成立。
2多个事件的相互独立性
（1）三个事件的独立性
定义 设A，B，C是三个事件，如果有
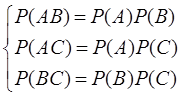
则称A，B，C两两独立。若还有P（ABC）＝P（A）P（B）P（C），则称A，B，C相互独立。
（2）n个事件的独立性
定义：设有n个事件A1，A2，…An，对任意的1≤i＜j＜k＜…≤n，如果以下等式均成立
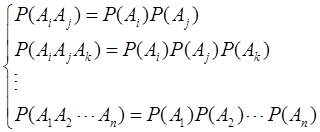
则称此n个事件A1，A2，…An相互独立。
获取方式：扫码关注下面公众号，关注后
回复关键词【清华大学821】或【清华大学概率论与统计学】
