复旦大学432统计学考研真题及辅导用书

考研真题

1. 全国名校应用统计硕士《432统计学》考研真题精选及详解

2. 应用统计硕士《432统计学》名校考研真题（2017年前）详解

考研指导书

1. 浙江大学《概率论与数理统计》（第5版）配套题库【考研真题精选＋章节题库】

浙江大学《概率论与数理统计》（第5版）配套题库【考研真题精选＋章节题库】

书籍目录

部分内容

第一部分　考研真题精选

一、选择题

1设A，B，C为三个随机事件，且P（A）＝P（B）＝P（C）＝1/4，P（AB）＝0，P（AC）＝P（BC）＝1/12，则A，B，C中恰有一个事件发生的概率为（　　）。[数一2020研]

A．3/4

B．2/3

C．1/2

D．5/12

【答案】D

【解析】只发生A事件的概率：

只发生B事件的概率：

只发生C事件的概率：

A，B，C中恰有一个事件发生的概率：

故选择D项。

2设A，B为随机事件，则P（A）＝P（B）的充分必要条件是（　　）。[数一2019研]

A．P（A∪B）＝P（A）＋P（B）

B．P（AB）＝P（A）P（B）

C．P（AB(＿)）＝P（BA(＿)）

D．

【答案】C

【解析】选项A只能说明事件A与事件B不相容，选项B只能说明事件A与事件B相互独立，并不能说明P（A）＝P（B），对选项D来说，若令B＝A(＿)，等式恒成立，亦不能说明P（A）＝P（B），故选C。

3若A，B为任意两个随机事件，则（　　）。[数一、数三2015研]

A．P（AB）≤P（A）P（B）

B．P（AB）≥P（A）P（B）

C．P（AB）≤（P（A）＋P（B））/2

D．P（AB）≥（P（A）＋P（B））/2

【答案】C

【解析】由于AB⊂A，AB⊂B，按概率的基本性质，有P（AB）≤P（A）且P（AB）≤P（B），从而P（AB）≤（P（A）＋P（B））/2，故选C项。

4设事件A，B相互独立，P（B）＝0.5，P（A－B）＝0.3则P（B－A）＝（　　）。[数一、数三2014研]

A．0.1

B．0.2

C．0.3

D．0.4

【答案】B

【解析】P（A－B）＝0.3＝P（A）－P（AB）＝P（A）－P（A）P（B）＝P（A）－0.5P（A）＝0.5P（A），故P（A）＝0.6，P（B－A）＝P（B）－P（AB）＝0.5－0.5P（A）＝0.2。

5设随机变量X与Y相互独立，且都服从正态分布N（μ，σ²），则P{|X－Y|＜1}（　　）。[数一2019研]

A．与μ无关，而与σ²有关

B．与μ有关，而与σ²无关

C．与μ，σ²都有关

D．与μ，σ²都无关

【答案】A

【解析】因为X，Y相互独立且都服从N（μ，σ²），记Z＝X－Y，则Z服从N（0，2σ²）分布，P{|Z|＜1}只与σ²有关，因此P{|X－Y|＜1}与μ无关，而与σ²有关，故选A。

6设随机变量X的概率密度f（x）满足f（1＋x）＝f（1－x），且

则P{X＜0}＝（　　）。[数一2018研]

A．0.2

B．0.3

C．0.4

D．0.5

【答案】A

【解析】由f（1＋x）＝f（1－x），知f（x）的图像关于x＝1对称，利用特殊值法：将f（x）看成随机变量X～N（1，σ²）的概率密度，根据正态分布的对称性，P{X＜0}＝0.2。

7设随机变量X～N（μ，σ²）（σ＞0），记p＝P{X≤μ＋σ²}，则（　　）。[数一2017研]

A．p随着μ的增加而增加

B．p随着σ的增加而增加

C．p随着μ的增加而减少

D．p随着σ的增加而减少

【答案】B

【解析】因为p＝P{X≤μ＋σ²}＝P{（X－μ）/σ≤σ}＝Φ（σ），所以p的大小与μ无关，随着σ的增大而增大。

8设X₁，X₂，X₃是随机变量，且X₁～N（0，1），X₂～N（0，2²），X₃～N（5，3²），P_i＝P{－2≤X_i≤2}（i＝1，2，3），则（　　）。[数一、数三2013研]

A．P₁＞P₂＞P₃

B．P₂＞P₁＞P₃

C．P₃＞P₁＞P₂

D．P₁＞P₃＞P₂

【答案】A

【解析】由X₁～N（0，1），X₂～N（0，2²），X₃～N（5，3²），知

P₁＝P{－2≤X₁≤2}＝P{|X₁|≤2}＝2Φ（2）－1

P₂＝P{－2≤X₂≤2}＝P{－1≤X₂/2≤1}＝P{|X₂/2|≤1}＝2Φ（1）－1

故P₁＞P₂，由X₃～N（5，3²）及概率密度的对称性知，P₁＞P₂＞P₃。

9设随机变量X的分布函数为，则P{X＝1}＝（　　）。[数一，数三2010研]

A．0

B．1/2

C．1/2－e^－1

D．1－e^－1

【答案】C

【解析】P{X＝1}＝F（1）－F（1－0）＝1－e^－1－1/2＝1/2－e^－1。

10设随机变量（X，Y）服从二维正态分布N（0，0；1，4；－1/2），下列随机变量中服从标准正态分布且与X独立的是（　　）[数三2020研]

A．

B．

C．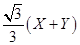

D．

【答案】C

【解析】由二维正态的性质知X＋Y～N（μ，σ²），因

μ＝E（X＋Y）＝E（X）＋E（Y）＝0

故

又服从二维正态分布，而

故与X不相关，由二维正态的性质知，与X独立。

故应选C项。

11设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X＜Y}＝（　　）。[数一2012研]

A．1/5

B．1/3

C．2/5

D．4/5

【答案】A

【解析】已知X～E（1），Y～E（4），故概率密度

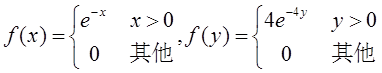
从而（X，Y）联合概率密度为

则

12设随机变量X，Y不相关，且EX＝2，EY＝1，DX＝3，则E[X（X＋Y－2）]＝（　　）。[数一2015研]

A．－3

B．3

C．－5

D．5

【答案】D

【解析】随机变量X，Y不相关，因此E（XY）＝E（X）E（Y），进而得

E[X（X＋Y－2）]＝E（X²＋XY－2X）＝E（X²）＋E（XY）－2E（X）＝D（X）＋E²（X）＋E（X）·E（Y）－2E（X）＝3＋2²＋2×1－2×2＝5

故选D项。

13设总体X～B（m，θ），X₁，X₂，…，X_n为来自该总体的简单随机样本，X(＿)为样本均值，则＝（　　）。[数三2015研]

A．（m－1）nθ（1－θ）

B．m（n－1）θ（1－θ）

C．（m－1）（n－1）θ（1－θ）

D．mnθ（1－θ）

【答案】B

【解析】根据样本方差的性质，有E（S²）＝D（X）＝mθ（1－θ）。

从而

故选B项。

14设连续型随机变量X₁，X₂相互独立，且方差均存在，X₁，X₂的概率密度分别为f₁（x），f₂（x），随机变量Y₁的概率密度为，随机变量Y₂＝（X₁＋X₂）/2，则（　　）。[数一2014研]

A．EY₁＞EY₂，DY₁＞DY₂

B．EY₁＝EY₂，DY₁＝DY₂

C．EY₁＝EY₂，DY₁＜DY₂

D．EY₁＝EY₂，DY₁＞DY₂

【答案】D

【解析】

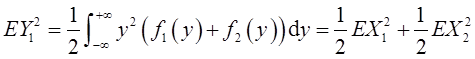
15设X₁，X₂，…，X_n（n≥2）为来自总体N（μ，σ²）（σ＞0）的简单随机样本，令

则（　　）。[数三2018研]

A．

B．

C．

D．

【答案】B

【解析】因为

所以

根据抽样定理得：

又X(＿)与S²相互独立，所以

16设X₁，X₂，…，X_n（n≥2）为来自总体N（μ，1）的简单随机样本，记，则下列结论中不正确的是（　　）。[数一2017研]

A．服从χ²分布

B．2（X_n－X₁）²服从χ²分布

C．服从χ²分布

D．n（X(＿)－μ）²服从χ²分布

【答案】B

【解析】A项，X_i－μ～N（0，1），故

B项

即（X_n－X₁）²/2～χ²（1）。

C项，由

D项，（X(＿)－μ）～N（0，1/n），则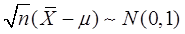，所以n（X(＿)－μ）²～χ²（1）。

17设X₁，X₂，X₃为来自正态总体N（0，σ²）的简单随机样本，则统计量服从的分布是（　　）。[数三2014研]

A．F（1，1）

B．F（2，1）

C．t（1）

D．t（2）

【答案】C

【解析】由题意知，，X₁－X₂～N（0，2σ²），，X₃～N（0，σ²），所以X₃/σ～N（0，1），X₃²/σ²～χ²（1），且与X₃/σ相互独立，故

获取方式：扫码关注下面公众号，关注后

回复关键词【复旦大学432】或【复旦大学统计学】