考研真题
1. 北京科技大学《876量子力学》历年考研真题汇总
2. 全国名校量子力学考研真题汇总
3. 2026年量子力学考研真题精解精析50题
考研指导书
1. 周世勋《量子力学教程》(第2版)笔记和课后习题(含考研真题)

北京科技大学《876量子力学》历年考研真题汇总
书籍目录
2014年北京科技大学876量子力学考研真题
2013年北京科技大学876量子力学考研真题
2012年北京科技大学876量子力学考研真题
2011年北京科技大学876量子力学考研真题
2010年北京科技大学876量子力学考研真题
2009年北京科技大学876量子力学考研真题
2008年北京科技大学876量子力学考研真题
2007年北京科技大学476量子力学考研真题
2006年北京科技大学476量子力学考研真题
2005年北京科技大学476量子力学B考研真题
2004年北京科技大学476量子力学B考研真题

部分内容
2014年北京科技大学876量子力学考研真题
试题编号: 876
试题名称: 量子力学
适用专业:
物理学
一、多选题(每题2分,共40分,答案可能是一个,也可能是多个):
1.以下哪个波函数表示的质量为m的非相对性粒子具有较高的能量:______
A.
B.
C.
D.
2.以下哪些函数是奇函数:______
A.
B.
C.狄拉克德尔塔函数
D.狄拉克德尔塔函数的一阶导数
3.“*”是取复共轭运算,以下算式正确的是:______
A.
B.
C.
D.
4.玻尔模型中,角动量量子化条件是:______
A.
B.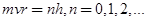
C. 
D. 
5.关于厄米矩阵,以下说法正确的是:______
A.对角线上的元素必定是实数
B.非对角线上的元素必定是实数
C.对角线上的元素可以是纯虚数
D.非对角线上的元素必须包含纯虚数
6.质量为m的粒子在宽度为L的一维无限深势阱中运动,基态能是:_________
A.
B. 
C. 
D. 
7.质量为m的粒子在宽度为L的一维无限深势阱中运动,基态波函数是:______
A.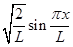
B.
C.
D.
8.对一维无限深势阱问题,解定态薛定谔方程,解出能量本征值是 ,对应的本征函数是
,对应的本征函数是 ,以下哪个波函数表示的是所谓“定态”:______
,以下哪个波函数表示的是所谓“定态”:______
A.
B.
C.
D.
9.定义平移算符为 ,这里
,这里 是动量算符,
是动量算符,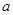 是位移参数,以下说法正确的是:______
是位移参数,以下说法正确的是:______
A.平移算符是厄米算符
B.平移算符是单位算符
C.平移算符是幺正算符
D.平移算符可以用来表示一个物理量
10.以下哪些算符一定是厄米算符:______
A.幺正算符
B.平移算符
C.投影算符
D.单位算符
11.假设 ,
, 是狄拉克右矢空间中的向量,以下说法正确的是:______
是狄拉克右矢空间中的向量,以下说法正确的是:______
A.
B.
C.
D.
12.假设 ,
, 是狄拉克右矢空间中的向量,以下哪些是算符:______
是狄拉克右矢空间中的向量,以下哪些是算符:______
A.
B.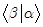
C.
D.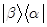
13.假设 ,
, 是狄拉克右矢空间中的向量,
是狄拉克右矢空间中的向量, ,
, 是复系数,
是复系数, ,以下哪些等式成立:_______
,以下哪些等式成立:_______
A.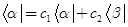
B. 
C. 
D. 
14.假设A是算符,但不一定是厄米算符,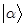 ,
, 是狄拉克右矢空间中的向量,以下哪些等式成立:______
是狄拉克右矢空间中的向量,以下哪些等式成立:______
A.
B. 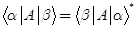
C.
D. 
15. 表象下,对
表象下,对 的量子态,以下说法正确的是:______
的量子态,以下说法正确的是:______
A. ,
, 同时取确定值
同时取确定值
B.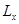 的取值是完全不确定的
的取值是完全不确定的
C. 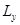 的取值是完全不确定的
的取值是完全不确定的
D. 的期望值是0
的期望值是0
16.自旋的泡利矩阵表示,以下哪些是厄米矩阵:______
A.
B.
C.
D.
17.自旋的泡利矩阵表示,哪些是幺正矩阵:______
A.
B.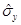
C.
D.
18.线性谐振子的占有数表象, ,
, 分别是产生和湮灭算符,以下哪些是厄米算符:______
分别是产生和湮灭算符,以下哪些是厄米算符:______
A.
B.
C.
D.
19.线性谐振子的占有数表象, ,
, 分别是产生和湮灭算符,以下哪些算式成立:______
分别是产生和湮灭算符,以下哪些算式成立:______
A.
B.
C.
D.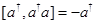
20.以下哪些态矢量表示的是“自旋三重态态”
:______
A.
B.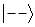
C.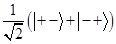
D.
二、简答题(每题5分,共50分):
1.在狄拉克记号下, 的物理含义是什么?
的物理含义是什么?
2.对一维空间, 的数学表达式是什么?
的数学表达式是什么?
3.请写出在位置表象下,位置算符和动量算符的表达式:
4.请写出在动量表象下,位置算符和动量算符的表达式:
5.假设 分别是位置算符,动量算符,请证明:
分别是位置算符,动量算符,请证明:
6.对厄米算符A,假设有本征值问题 ,请证明
,请证明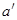 一定是实数。
一定是实数。
7.假设A,B是厄米算符, ,请写出严格的不确定关系。
,请写出严格的不确定关系。
8.假设A,B是厄米算符,请证明: 一定是厄米算符。
一定是厄米算符。
9.请写出 的共同本征态
的共同本征态 所满足的共同本征值问题;对
所满足的共同本征值问题;对 的取值有何限制?
的取值有何限制?
10.质量为m的非相对论粒子在势场V中运动,请写出相应的含时薛定谔方程。请继续写出粒子流密度 的表达式和粒子数守恒的微分形式的表达式。
的表达式和粒子数守恒的微分形式的表达式。
三、计算和证明(每题10分,共60分):
1.两个全同电子在宽度为L的一维无限深势阱中运动,考虑电子的自旋,假设电子的质量是m,单电子在一维无限深势阱中的能量本征值是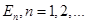 ,n=1是基态,n=2是第一激发态,……,忽略“电子-电子”间相互作用,(1)系统的基态能是多少?(2)第一激发态的能量本征值是多少?(3)假设
,n=1是基态,n=2是第一激发态,……,忽略“电子-电子”间相互作用,(1)系统的基态能是多少?(2)第一激发态的能量本征值是多少?(3)假设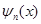 是与
是与 相对应的电子轨道部分的波函数,请写出系统的基态波函数。(提示:写成轨道部分和自旋部分乘积的形式)
相对应的电子轨道部分的波函数,请写出系统的基态波函数。(提示:写成轨道部分和自旋部分乘积的形式)
2.氢原子的波函数可表示为: ,这里主量子数
,这里主量子数 的取值范围是?角动量量子数
的取值范围是?角动量量子数 的取值范围是?磁量子数
的取值范围是?磁量子数 的取值范围是?自旋量子数
的取值范围是?自旋量子数 的取值范围是?并请证明对主量子数
的取值范围是?并请证明对主量子数 简并度
简并度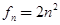 。
。
3.对于 的共同本征态
的共同本征态 ,证明:(1)
,证明:(1) ;(2)
;(2)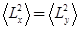 ;(3)对
;(3)对 验证满足不确定关系。
验证满足不确定关系。
4.自旋泡利矩阵, 表象下,对
表象下,对 ,求解本征值问题,即求出
,求解本征值问题,即求出 对应的本征值和本征向量,假设量子态
对应的本征值和本征向量,假设量子态 ,求对此量子态观测到
,求对此量子态观测到 的几率。
的几率。
5.氢原子基态波函数的径向部分是 ,(1)求归一化因子A;(2)当r=?时,径向部分的概率分布达到最大。
,(1)求归一化因子A;(2)当r=?时,径向部分的概率分布达到最大。
6.两个自旋1/2耦合,哈密顿量是: ,假设
,假设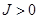 ,
, ,求系统的基态能和基态波函数。
,求系统的基态能和基态波函数。
更多内容,请点击获取:
http://shuyue.100xuexi.com/Ebook/969920.html
