北京大学431金融学综合考研真题及辅导用书

考研真题

1. 北京大学光华管理学院《431金融学综合》[专业硕士]历年考研真题汇总

2. 北京大学经济学院《431金融学综合》[专业硕士]历年考研真题汇总

3. 北京大学数学科学学院《431金融学综合》历年考研真题汇总（回忆版）

4. 全国名校金融硕士《431金融学综合》考研真题精选及详解（部分视频讲解）

5. 金融硕士《431金融学综合》名校考研真题汇总（含部分答案）（2017年前）

考研指导书

1. 范里安《微观经济学：现代观点》（第9版）笔记和课后习题详解

2. 范里安《微观经济学：现代观点》（第9版）名校考研真题详解

3. 范里安《微观经济学：现代观点》（第9版）配套题库【考研真题精选＋章节题库】

4. 钟根元《中级微观经济学学习指南》（第4版）练习题详解

5. 平新乔《微观经济学十八讲》课后习题和强化习题详解

6. 尼科尔森《微观经济理论——基本原理与扩展》（第11版）笔记和课后习题详解

7. 尼科尔森《微观经济理论——基本原理与扩展》（第11版）配套题库【考研真题精选＋章节题库】

8. 茆诗松《概率论与数理统计教程》（第3版）笔记和课后习题（含考研真题）详解

9. 茆诗松《概率论与数理统计教程》（第3版）配套题库【考研真题精选＋章节题库】

10. 古扎拉蒂《计量经济学基础》（第5版）课后习题详解

11. 黄达《金融学》（第5版）笔记和课后习题（含考研真题）详解

12. 黄达《金融学》（第5版）配套题库【考研真题精选＋章节题库】

13. 曹凤岐《证券投资学》（第3版）配套题库【考研真题精选＋章节题库】

14. 罗斯《公司理财》（第11版）笔记和课后习题详解

15. 罗斯《公司理财》（第11版）配套题库【考研真题精选＋章节题库】

16. 博迪《投资学》（第10版）笔记和课后习题详解

17. 博迪《投资学》（第10版）配套题库【考研真题精选＋章节题库】

18. 姚长辉《货币银行学》（第5版）配套题库【考研真题精选＋章节题库】

茆诗松《概率论与数理统计教程》（第3版）配套题库【考研真题精选＋章节题库】

书籍目录

部分内容

第一部分　考研真题精选

一、选择题

1设A，B，C为三个随机事件，且P（A）＝P（B）＝P（C）＝1/4，P（AB）＝0，P（AC）＝P（BC）＝1/12，则A，B，C中恰有一个事件发生的概率为（　　）。[数一2020研]

A．3/4

B．2/3

C．1/2

D．5/12

【答案】D

【解析】只发生A事件的概率：

只发生B事件的概率：

只发生C事件的概率：

A，B，C中恰有一个事件发生的概率：

故选择D项。

2设A，B为随机事件，则P（A）＝P（B）的充分必要条件是（　　）。[数一2019研]

A．P（A∪B）＝P（A）＋P（B）

B．P（AB）＝P（A）P（B）

C．P（AB(＿)）＝P（BA(＿)）

D．

【答案】C

【解析】选项A只能说明事件A与事件B不相容，选项B只能说明事件A与事件B相互独立，并不能说明P（A）＝P（B）。对选项D来说，若令B＝A(＿)，等式恒成立，亦不能说明P（A）＝P（B），故选C。

3设事件A，B相互独立，P（B）＝0.5，P（A－B）＝0.3，则P（B－A）＝（　　）。[数一、数三2014研]

A．0.1

B．0.2

C．0.3

D．0.4

【答案】B

【解析】P（A－B）＝0.3＝P（A）－P（AB）＝P（A）－P（A）P（B）＝P（A）－0.5P（A）＝0.5P（A），故P（A）＝0.6，P（B－A）＝P（B）－P（AB）＝0.5－0.5P（A）＝0.2。

4设随机变量X与Y相互独立，且都服从正态分布N（μ，σ²），则P{|X－Y|＜1}（　　）。[数一2019研]

A．与μ无关，而与σ²有关

B．与μ有关，而与σ²无关

C．与μ，σ²都有关

D．与μ，σ²都无关

【答案】A

【解析】因为X，Y相互独立且都服从N（μ，σ²），记Z＝X－Y，则Z服从N（0，2σ²）分布。P{|Z|＜1}只与σ²有关，因此P{|X－Y|＜1}与μ无关，而与σ²有关。故选A。

5设随机变量X的概率密度f（x）满足f（1＋x）＝f（1－x），且

则P{X＜0}＝（　　）。[数一2018研]

A．0.2

B．0.3

C．0.4

D．0.5

【答案】A

【解析】由f（1＋x）＝f（1－x），知f（x）的图像关于x＝1对称，利用特殊值法：将f（x）看成随机变量X～N（1，σ²）的概率密度，根据正态分布的对称性，P{X＜0}＝0.2。

6设随机变量X～N（μ，σ²）（σ＞0），记p＝P{X≤μ＋σ²}，则（　　）。[数一2016研]

A．p随着μ的增加而增加

B．p随着σ的增加而增加

C．p随着μ的增加而减少

D．p随着σ的增加而减少

【答案】B

【解析】因为p＝P{X≤μ＋σ²}＝P{（X－μ）/σ≤σ}＝Φ（σ），所以p的大小与μ无关，随着σ的增大而增大。

7设连续型随机变量X₁，X₂相互独立，且方差均存在，X₁，X₂的概率密度分别为f₁（x），f₂（x），随机变量Y₁的概率密度为，随机变量Y₂＝（X₁＋X₂）/2，则（　　）。[数一2014研]

A．EY₁＞EY₂，DY₁＞DY₂

B．EY₁＝EY₂，DY₁＝DY₂

C．EY₁＝EY₂，DY₁＜DY₂

D．EY₁＝EY₂，DY₁＞DY₂

【答案】D

【解析】

DY₁＝E（Y₁²）－E²（Y₁）＝EX₁²/2＋EX₂²/2－E²（X₁）/4－E²（X₂）/4－E（X₁）E（X₂）/2＝D（X₁）/4＋D（X₂）/4＋E（X₁－X₂）²/4≥D（X₁）/4＋D（X₂）/4＝DY₂

8设X₁，X₂，X₃是随机变量，且X₁～N（0，1），X₂～N（0，2²），X₃～N（5，3²），P_j＝P{－2≤X_j≤2}（j＝1，2，3）则（　　）。[数一、数三2013研]

A．P₁＞P₂＞P₃

B．P₂＞P₁＞P₃

C．P₃＞P₁＞P₂

D．P₁＞P₃＞P₂

【答案】A

【解析】若X～N（μ，σ²），则（X－μ）/σ～N（0，1），故

P₁＝2Φ（2）－1，P₂＝P{－2≤X₂≤2}＝P{－1≤X₂/2≤1}＝2Φ（1）－1，则P₁＞P₂；

P₃＝P{－2≤X₃≤2}＝P{（－2－5）/3≤（X₃－5）/3≤（2－5）/3}＝Φ（－1）－Φ（－7/3）＝Φ（7/3）－Φ（1）

P₃－P₂＝1＋Φ（7/3）－3Φ（1）＜2－3Φ（1）＜0，故P₂＞P₃。

9设F₁（x），F₂（x）为两个分布函数，其相应的概率密度f₁（x），f₂（x）是连续函数，则必为概率密度的是（　　）。[数一、数三2011研]

A．f₁（x）f₂（x）

B．2f₂（x）F₁（x）

C．f₁（x）F₂（x）

D．f₁（x）F₂（x）＋f₂（x）F₁（x）

【答案】D

【解析】四个选项均满足大于等于零的条件，由D选项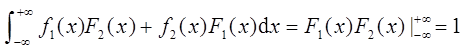而易知，D项满足连续分布概率密度的条件，为概率密度（其他选项均无法验证满足（－∞，＋∞）上积分为1的条件）。

10设随机变量（X，Y）服从二维正态分布N（0，0；1，4；－1/2），下列随机变量中服从标准正态分布且与X独立的是（　　）[数三2020研]

A．

B．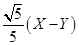

C．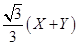

D．

【答案】C

【解析】由二维正态的性质知X＋Y～N（μ，σ²），因

μ＝E（X＋Y）＝E（X）＋E（Y）＝0

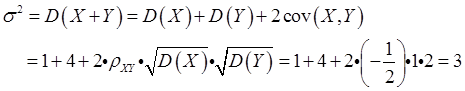
故

又服从二维正态分布，而

故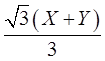与X不相关，由二维正态的性质知，与X独立。

故应选C项。

11随机试验E有三种两两不相容的结果A₁，A₂，A₃，且三种结果发生的概率均为1/3。将试验E独立重复做2次，X表示2次试验中结果A₁发生的次数，Y表示2次试验中结果A₂发生的次数，则X与Y的相关系数为（　　）。[数一2016研]

A．－1/2

B．－1/3

C．1/3

D．1/2

【答案】A

【解析】由题可求出X，Y的联合分布概率如表1所示。

表1

所以，EX＝0×4/9＋1×4/9＋2×1/9＝2/3。同理EY＝2/3，EX²＝8/9，EY²＝8/9，EXY＝2/9。Cov（X，Y）＝EXY－EXEY＝－2/9。DX＝EX²－（EX）²＝4/9，DY＝EY²－（EY）²＝4/9。所以

12设随机变量X与Y相互独立，且X～N（1，2），Y～N（1，4），则D（XY）＝（　　）。[数三2016研]

A．6

B．8

C．14

D．15

【答案】C

【解析】根据题意，X、Y相互独立，则D（XY）＝E（XY）²－（EXY）²＝EX²EY²－（EXEY）²＝[DX＋（EX）²][DY＋（EY）²]－（EXEY）²＝14。

13将长度为1m的木棒随机地截成两段，则两段长度的相关系数为（　　）。[数一2012研]

A．1

B．1/2

C．－1/2

D．－1

【答案】D

【解析】假设木棒两段长度分别为x，y，有x＋y＝1即y＝1－x，故x，y是线性关系，且相关系数为－1。

14设随机变量X与Y相互独立，且分别服从参数为1与参数为4的指数分布，则P{X＜Y}＝（　　）。[数一2012研]

A．1/5

B．1/3

C．2/5

D．4/5

【答案】A

【解析】已知X～E（1），Y～E（4）。故概率密度

从而（X，Y）联合概率密度为

则

15设随机变量X与Y相互独立，且都服从区间（0，1）上的均匀分布，则P{X²＋Y²≤1}＝（　　）。[数三2012研]

A．1/4

B．1/2

C．π/8

D．π/4

【答案】D

【解析】由题意知X～U（0，1），Y～U（0，1）且相互独立，则

由图1，得

图1

16设随机变量X与Y相互独立，且EX与EY存在。记U＝max{X，Y}，V＝min{X，Y}则E（UV）等于（　　）。[数一2011研]

A．EU·EV

B．EX·EY

C．EU·EY

D．EX·EV

【答案】B

【解析】UV＝max{X，Y}min{X，Y}，而无论X与Y的关系如何，UV＝XY。从而E（UV）＝E（XY）＝EX·EY。

17设X₁，X₂，…，X_n为来自总体X的简单随机样本，其中P（X＝0）＝P（X＝1）＝1/2，Φ（x）表示标准正态分布函数，则利用中心极限定理可得的近似值为（　　）。[数一2020研]

A．1－Φ（1）

B．Φ（1）

C．1－Φ（2）

D．Φ（2）

【答案】B

【解析】E（X）＝1/2，D（X）＝1/4，，，将标准化可得，由中心极限定理可知近似服从标准正态分布，，故选B项。

18设X₁，X₂，…，X_n（n≥2）为来自总体N（μ，σ²）（σ＞0）的简单随机样本，令

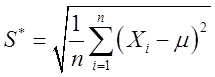
则（　　）。[数三2018研]

A．

B．

C．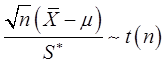

D．

【答案】B

【解析】因为

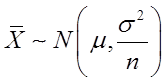
所以

根据抽样定理得：

又X(＿)与S²相互独立，所以

19设X₁，X₂，…，X_n（n≥2）为来自总体N（μ，1）的简单随机样本，记，则下列结论中不正确的是（　　）。[数一2017研]

A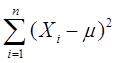．服从χ²分布

B．2（X_n－X₁）²服从χ²分布

C．服从χ²分布

D．n（X(＿)－μ）²服从χ²分布

【答案】B

【解析】A项，X_i－μ～N（0，1），故

B项，

即（X_n－X₁）²/2～χ²（1）。

C项，由

D项，（X(＿)－μ）～N（0，1/n），则，所以n（X(＿)－μ）²～χ²（1）。

20设X₁，X₂，X₃为来自正态总体N（0，σ²）的简单随机样本，则统计量服从的分布是（　　）。[数三2014研]

A．F（1，1）

B．F（2，1）

C．t（1）

D．t（2）

【答案】C

【解析】由题意知，，X₁－X₂～N（0，2σ²），，X₃～N（0，σ²），所以X₃/σ～N（0，1），X₃²/σ²～χ²（1），且与X₃/σ相互独立，故

21给定总体X～N（μ，σ²），σ²已知，给定随机样本X₁，X₂，…，X_n，对总体均值μ进行检验，令H₀：μ＝μ₀，H₁：μ≠μ₀，则（　　）。[数一2018研]

A．若显著性水平α＝0.05时拒绝H₀，则α＝0.01时必拒绝H₀

B．若显著性水平α＝0.05时拒绝H₀，则α＝0.01时必接受H₀

C．若显著性水平α＝0.05时接受H₀，则α＝0.01时必拒绝H₀

D．若显著性水平α＝0.05时接受H₀，则α＝0.01时必接受H₀

【答案】D

【解析】令

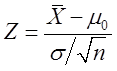
X(＿)～N（μ，σ²/n），故当假设H₀为真时，Z～N（0，1）。当α＝0.05时，拒绝域为

其中z_0.025为上0.025分位点。α＝0.05对应的接受域为

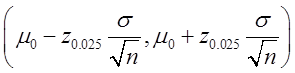
当α＝0.01时，拒绝域为

其中z_0.025为上0.005分位点。α＝0.01对应的接受域为

又由于z_0.025＜z_0.005，所以α＝0.05对应的接受域包含于α＝0.01对应的接受域。当显著性水平α＝0.05时，接受H₀，那么当显著性水平α＝0.01时，必接受H₀，D项正确。

获取方式：扫码关注下面公众号，关注后

回复关键词【北京大学431】或【北京大学金融学综合】