考研真题
1. 北京大学光华管理学院《431金融学综合》[专业硕士]历年考研真题汇总
2. 北京大学经济学院《431金融学综合》[专业硕士]历年考研真题汇总
3. 北京大学数学科学学院《431金融学综合》历年考研真题汇总(回忆版)
4. 全国名校金融硕士《431金融学综合》考研真题精选及详解(部分视频讲解)
5. 金融硕士《431金融学综合》名校考研真题汇总(含部分答案)(2017年前)
考研指导书
1. 范里安《微观经济学:现代观点》(第9版)笔记和课后习题详解
2. 范里安《微观经济学:现代观点》(第9版)名校考研真题详解
3. 范里安《微观经济学:现代观点》(第9版)配套题库【考研真题精选+章节题库】
4. 钟根元《中级微观经济学学习指南》(第4版)练习题详解
5. 平新乔《微观经济学十八讲》课后习题和强化习题详解
6. 尼科尔森《微观经济理论——基本原理与扩展》(第11版)笔记和课后习题详解
7. 尼科尔森《微观经济理论——基本原理与扩展》(第11版)配套题库【考研真题精选+章节题库】
8. 茆诗松《概率论与数理统计教程》(第3版)笔记和课后习题(含考研真题)详解
9. 茆诗松《概率论与数理统计教程》(第3版)配套题库【考研真题精选+章节题库】
10. 古扎拉蒂《计量经济学基础》(第5版)课后习题详解
11. 黄达《金融学》(第5版)笔记和课后习题(含考研真题)详解
12. 黄达《金融学》(第5版)配套题库【考研真题精选+章节题库】
13. 曹凤岐《证券投资学》(第3版)配套题库【考研真题精选+章节题库】
14. 罗斯《公司理财》(第11版)笔记和课后习题详解
15. 罗斯《公司理财》(第11版)配套题库【考研真题精选+章节题库】
16. 博迪《投资学》(第10版)笔记和课后习题详解
17. 博迪《投资学》(第10版)配套题库【考研真题精选+章节题库】
18. 姚长辉《货币银行学》(第5版)配套题库【考研真题精选+章节题库】

平新乔《微观经济学十八讲》课后习题和强化习题详解
书籍目录
第1讲 偏好、效用与消费者的基本问题
第2讲 间接效用函数与支出函数
第3讲 价格变化对消费者的配置效应与福利效应
第4讲 VNM效用函数与风险升水
第5讲 风险规避、风险投资与跨期决策
第6讲 生产函数与规模报酬
第7讲 要素需求函数、成本函数、利润函数与供给函数
第8讲 完全竞争与垄断
第9讲 古诺(Cournot)均衡、Bertrand与不完全竞争
第10讲 策略性博弈与纳什均衡
第11讲 广延型博弈与反向归纳策略
第12讲 子博弈与完美性
第13讲 委托-代理理论初步
第14讲 信息不对称、逆向选择与信号博弈
第15讲 工资、寻找工作与劳动市场中的匹配
第16讲 一般均衡与福利经济学的两个基本定理
第17讲 外在性、科斯定理与公共品理论
第18讲 企业的性质、边界与产权

部分内容
第1讲 偏好、效用与消费者的基本问题
1.1 课后习题详解
1根据下面的描述,画出消费者的无差异曲线。对于(2)和(3)题,写出效用函数。
(1)王力喜欢喝汽水x,但是厌恶吃冰棍y。
(2)李楠既喜欢喝汽水x,又喜欢吃冰棍y,但她认为三杯汽水和两根冰棍是无差异的。
(3)萧峰有个习惯,他每喝一杯汽水x就要吃两根冰棍y,当然汽水和冰棍对他而言是多多益善。
(4)杨琳对于有无汽水x喝毫不在意,但她喜欢吃冰棍y。
答:(1)根据题意,对王力而言,冰棒是厌恶品,相应的无差异曲线如图1-1所示(图中箭头表示更高的效用方向)。
(2)根据题意,对李楠而言,汽水和冰棒是完全替代品,其效用函数为u(x,y)=2x+3y,相应的无差异曲线如图1-2所示。
(3)消费者对这两种商品的效用函数为u(x,y)=min{x,y/2},如图1-3所示。
(4)如图1-4所示,其中x为中性品。

图1-1 喜欢喝汽水厌恶吃冰棍

图1-2 既喜欢喝汽水又喜欢吃冰棍

图1-3 喝一杯汽水就要吃两根冰棍

图1-4 对于有无汽水喝毫不在意
2作图:如果一个人的效用函数为u(x1,x2)=max{x1,x2}。
(1)请画出三条无差异曲线。
(2)如果p1=1,p2=2,y=10。请在图1-5上找出该消费者的最优的消费组合。
答:(1)由效用函数画出的三条无差异曲线如图1-5所示。

图1-5 无差异曲线和最优点
(2)效用函数确定了消费者的最优选择必定是落在便宜的商品上,即他会将所有收入都用于购买相对便宜的商品,最优点如图1-5中的A点所示,在该点此人消费10个单位的x1,0个单位的x2。
3下列说法对吗?为什么?
若某个消费者的偏好可以由效用函数u(x1,x2)=10(x12+2x1x2+x22)-50来描述,那么对此消费者而言,商品1和商品2是完全替代的。
答:此说法正确。理由如下:
方法一:由于效用函数的单调变换和原效用函数表示同一个偏好,所以对u进行如下单调变换f(u)=[(u+50)/10]1/2后,得到新的效用函数为u′(x1,x2)=x1+x2,这是完全替代偏好的效用函数,所以原效用函数所描述的偏好中,商品1与商品2也是完全替代的。
方法二:由题意知:MU1=20x1+20x2,MU2=20x1+20x2;
边际替代率MRS12=MU1/MU2=(20x1+20x2)/(20x1+20x2)=1是一个常数,所以商品1与商品2是以1∶1的比率完全替代的。
4设u(x1,x2)=(lnx1)/2+(lnx2)/2,这里x1,x2∈R+。
(1)证明:x1与x2的边际效用都递减。
(2)请给出一个效用函数形式,但该形式不具备边际效用递减的性质。
答:(1)将u关于x1和x2分别求二阶偏导数得∂2u/∂x12=-1/(2x12)<0,∂2u/∂x22=-1/(2x22)<0,所以x1与x2的边际效用都递减。
(2)如效用函数u(x1,x2)=x12+x22,它关于x1与x2的二阶偏导数恒大于零,所以x1与x2的边际效用都是递增的。只要效用函数的二阶导数不为负,就可以保证边际效用不是递减的。
5常替代弹性效用函数u(x1,x2)=(α1x1ρ+α2x2ρ)1/ρ,请证明:
(1)当ρ=1,该效用函数为线性。
(2)当ρ→0时,该效用函数趋近于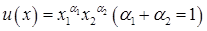 。
。
(3)当ρ→-∞时,该效用函数趋近于u(x)=min{x1,x2}。
证明:(1)当ρ=1时,u(x1,x2)=α1x1+α2x2,此时函数是线性的。
(2)

(3)

最后一个符号用到洛必达法具,下面分情况讨论:
①当x1>x2时:

上式中倒数第二个等号成立是因为当x1/x2>1时, 。
。
②当x1<x2时:

③当x1=x2时,有u(x)=x1=x2=min{x1,x2}。
综上可知:

6茜茜总喜欢在每一杯咖啡里加两汤匙糖。如果每汤匙糖的价格是p1,每杯咖啡的价格是p2,消费者花费M元在咖啡和糖上,那么,她将打算购买多少咖啡和糖?如果价格变为p1′和p2′,对她关于咖啡和糖的消费会发生什么影响?
答:(1)由于茜茜总喜欢在每一杯咖啡里加两汤匙糖,所以咖啡和糖对茜茜而言是完全互补品,如果用c和s分别表示她消费的咖啡的数量(以杯为单位)和糖的数量(以汤匙为单位),那么她的效用函数就可以表示为:u(c,s)=min{c,s/2}。
从而她的效用最大化问题可以表示为:

对于最优选择,必有c=s/2。这是因为如果c>s/2,那么在保持预算约束不变的条件下,减少一些糖的消费,再增加一些咖啡的消费,就可以提高茜茜的效用,如图1-6的A点所示。所以对于最优选择,c>s/2一定不成立;对于c<s/2也有类似的理由。

图1-6 互补偏好的最优选择
再结合预算约束,就可以得到消费者的最优消费量为:
c=M/(2p1+p2),s=2M/(2p1+p2)
(2)当价格变为p1′和p2′时,茜茜对咖啡和糖的消费变为:
c=M/(2p1′+p2′),s=2M/(2p1′+p2′)
所以咖啡和糖两者之中任何一个价格上涨都会引起茜茜对它们的需求同时下降。
7令 表示偏好关系,
表示偏好关系, 表示严格偏好关系,
表示严格偏好关系, 表示无差异关系,证明下列关系:
表示无差异关系,证明下列关系:
(1)
(2)
(3)
(4)
答:(1) 的含义是:弱偏好本身是弱偏好的一个子集。
的含义是:弱偏好本身是弱偏好的一个子集。
根据子集的定义,任何非空集合都是自己的一个子集。由于偏好关系是定义在选择集的二次幂集上的完备的序关系,又由选择集的非空性质得到选择集二次幂集的非空性,得到偏好关系的非空性质。
(2) 的含义是:如果A和B之间无差异,那么A至少和B一样好,从而本结论成立。
的含义是:如果A和B之间无差异,那么A至少和B一样好,从而本结论成立。
(3) 的含义是:如果消费者对A的偏好超过了对B的偏好这一关系和消费者对A和B的偏好是无差异的这一关系中有一个成立,那么消费者对A的偏好至少和B一样好这一关系一定成立,反之亦然。根据
的含义是:如果消费者对A的偏好超过了对B的偏好这一关系和消费者对A和B的偏好是无差异的这一关系中有一个成立,那么消费者对A的偏好至少和B一样好这一关系一定成立,反之亦然。根据 关系的定义可知这个结论是成立的。
关系的定义可知这个结论是成立的。
(4) 的含义是:消费者对A的偏好超过了对B的偏好这一关系和消费者对A和B的偏好是无差异的这一关系不能同时成立。理由如下:如果
的含义是:消费者对A的偏好超过了对B的偏好这一关系和消费者对A和B的偏好是无差异的这一关系不能同时成立。理由如下:如果 和
和 同时成立,那么就有
同时成立,那么就有 ,从而得到
,从而得到 ,矛盾。
,矛盾。
8证明下列结论(或用具说服力的说理证明)
(1)“ ”与“
”与“ ”都不具有“完备性”。
”都不具有“完备性”。
(2)“ ”满足反省性。
”满足反省性。
(3)严格偏好关系不满足反省性。
(4)对于任何X中的x1与x2,在下列关系中只能居其一: ,或
,或 ,或
,或 。
。
证明:(1)“ ”与“
”与“ ”都不具有完备性。理由如下:
”都不具有完备性。理由如下:
如果一种偏好关系具有完备性,那么对消费集中任意两个消费束之间都可以建立这种关系。“ ”表示严格偏好关系,但是对任意的两个消费束A和B,消费者对他们可能是无差异的,这时A和B之间就不能建立严格偏好的关系。“
”表示严格偏好关系,但是对任意的两个消费束A和B,消费者对他们可能是无差异的,这时A和B之间就不能建立严格偏好的关系。“ ”表示无差异关系,但是对任意的两个消费束A和B,消费者可能严格偏好于A,这时A和B之间就不能建立无差异的关系。
”表示无差异关系,但是对任意的两个消费束A和B,消费者可能严格偏好于A,这时A和B之间就不能建立无差异的关系。
(2)“ ”满足反省性。理由如下:
”满足反省性。理由如下:
反省性是说,如果消费束A和消费束B之间满足某种二元关系,那么B和A之间也满足这种关系。如果A和B之间是无差异的,那么显然,B和A之间也是无差异的,所以“ ”满足反省性。
”满足反省性。
(3)严格偏好关系不满足反省性,理由如下:
如果消费者对A的偏好超过了对B的偏好,即 ,那么根据反省性,消费者对B的偏好也超过了对A的偏好,即
,那么根据反省性,消费者对B的偏好也超过了对A的偏好,即 。从而就有
。从而就有 ,即消费者对A的偏好超过了他对A的偏好,这样就出现了矛盾。所以严格偏好关系必然不满足反省性。
,即消费者对A的偏好超过了他对A的偏好,这样就出现了矛盾。所以严格偏好关系必然不满足反省性。
(4)对于X中的任何x1与x2,下列关系中只有一个能成立: ,或
,或 ,或
,或 。理由如下:
。理由如下:
如果这三种关系中至少有两个同时成立,那么共有以下四种情况:
① 且
且 ,由此可以得到
,由此可以得到 ,即
,即 ,矛盾!
,矛盾!
② 且
且 ,由此可以得到
,由此可以得到 ,即
,即 ,矛盾!
,矛盾!
③ 且
且 ,由此可以得到
,由此可以得到 ,即
,即 ,矛盾!
,矛盾!
④ ,
,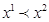 且
且 ,由此可以得到
,由此可以得到 ,即
,即 ,矛盾!
,矛盾!
综上可知这三种关系中只有一个能成立。
9一个只消费两类物品的消费者面临正的价格,其拥有正的收入,他的效用函数为
u(x1,x2)=x1
导出其马歇尔需求函数。
答:消费者的效用最大化问题为:

由约束条件可知x1=(y-p2x2)/p1,从而当x1=y/p1,x2=0时,消费者效用达到最大,从而该消费者的马歇尔需求函数为:x1=y/p1,x2=0。
10一个人的效用函数为u(x1,x2)=Ax1αx21-α,这里0<α<1,A>0。假定存在内点解,请推导其马歇尔需求函数。
答:该消费者的效用最大化问题为:

该问题的拉格朗日函数为:
L(x1,x2,λ)=Ax1αx21-α+λ(y-p1x1-p2x2)
使L(·)最大化的x1,x2,λ满足一阶条件:
∂L/∂x1=αAx1α-1x21-α-λp1=0①
∂L/∂x2=(1-α)Ax1αx2-α-λp2=0②
∂L/∂λ=y-x1p1-x2p2=0③
①式除以②式,得:
αx2/[(1-α)x1]=p1/p2
即:
x2=p1x1(1-α)/(p2α)④
④式代入③式得:
x1=αy/p1⑤
⑤式代入④式得:
x2=(1-α)y/p2⑥
那么⑤、⑥两式即为x1和x2的马歇尔需求函数。
11在下列效用函数形式里,哪些是效用函数的单调变换?
(1)u=2v-13。
(2)u=-1/v2。
〔3〕u=-1/v2。
(4)u=lnv。
(5)u=-e-v。
(6)u=v2。
(7)u=v2,对于v>0。
(8)u=v2,对于v<0。
答:当u1>u2意味着f(u1)>f(u2),则称f(u)为原效用函数u(x)的单调变换。本质上说,单调变换与一个单调函数是一回事。一个效用函数是原效用函数的单调变换,则该效用函数严格的单调递增。
(1)是单调变换。因为∂u/∂v=2>0。
(2)在v>0时是单调变换,v<0时不是单调变换。理由如下:
因为∂u/∂v=2/v3,所以当v>0时,∂u/∂v>0;当v<0时,∂u/∂v<0。从而只有当v>0时,u=-1/v2才是单调变换。
(3)在v>0时不是单调变换,v<0时,是单调变换。理由类似于(2)。
(4)在v>0时是单调变换,v<0时不是单调变换。因为当v<0时,函数lnv无意义。
(5)是单调变换。理由类似于(1)。
(6)在v>0时是单调变换,v<0时不是单调变换。理由类似于(2)。
(7)是单调变换。理由类似于(1)。
(8)不是单调变换。因为当v<0时,∂u/∂v=2v<0。
获取方式:扫码关注下面公众号,关注后

回复关键词【北京大学431】或【北京大学金融学综合】
