北京大学电子信息基础考研真题及辅导用书

考研真题

1. 全国名校电子技术基础（含模拟、数字）考研真题汇总

考研指导书

1. 康华光《电子技术基础-数字部分》（第6版）笔记和课后习题（含考研真题）详解

2. 康华光《电子技术基础-数字部分》（第6版）配套题库【考研真题精选＋章节题库】

康华光《电子技术基础-数字部分》（第6版）笔记和课后习题（含考研真题）详解

书籍目录

部分内容

第1章　数字逻辑概论

1.1　复习笔记

本章是《电子技术基础数字部分》的开篇，主要讲述了模拟信号和数字信号以及数字信号的描述方法，进而讨论了数制、二进制的算术运算、二进制代码和数字逻辑的基本运算，是整本教材的学习基础。笔记所列内容，读者应力求理解和熟练运用。

一、模拟信号与数字信号

1模拟信号和数字信号（见表1-1-1）

表1-1-1　模拟信号和数字信号

2数字信号的描述方法（见表1-1-2）

表1-1-2　数字信号的描述方法

3数字波形详细特征

（1）数字波形的两种类型见表1-1-3

表1-1-3　数字波形的类型

（2）周期性和非周期性

与模拟信号波形相同，数字波形亦有周期型和非周期性之分。周期性数字波形常用周期T和频率f来描述。脉冲波形的脉冲宽度用表示，所以占空比

（3）实际数字信号波形

在实际的数字系统中，数字信号并不理想。当从低电平跳变到高电平，或从高电平跳到低电平时，边沿没有那么陡峭，而要经历一个过渡过程。图1-1-1为非理想脉冲波形。

图1-1-1　非理想脉冲波形

（4）波形图、时序图或定时图

波形图、时序图或定时图概述见表1-1-4。

表1-1-4　波形图、时序图或定时图概述

时序图和定时图区别与特征见表1-1-5。

表1-1-5　时序图、定时图特征

二、数制

1几种常用的进制（见表1-1-6）

表1-1-6　几种常用的进制

2进制之间的转换

（1）其他进制转十进制

任意一个其他进制数转化成十进制可用如下表达式表示：

其中R表示进制，Ki表示相应位的值。例如（二进制转十进制）：（1011.01）₂＝1×2³＋0×2²＋1×2¹＋1×2⁰＋0×2^－1＋1×2^－2＝（11.25）₁₀。

（2）十进制转二进制

①整数部分的转换：将十进制数除以2，取所余数为k₀；将其商再除以2，取其余数为k₁，……以此类推，直到所得商等于0为止，余数k_n…k₁k₀（从下往上排）即为二进制数。以273.69为例，如图1-1-2所示。

②小数部分的转换：将十进制数乘以2，取乘积的整数部分为k_-1；将乘积的小数部分再乘以2，取乘积的整数部分为k_-2，……以此类推，直到求出要求的位数为止，k_-1k_-2k_-3…（从上往下排）即为二进制数。以273.69为例，如图1-1-3所示。

图1-1-2　十→二进制整数部分的转换

图1-1-3　十→二进制小数部分的转换

所以

十进制转其他进制也可以同样的方式以此类推。

（3）二进制与十六进制之间的相互转换

①二进制转十六进制：整数部分从低位到高位每4位二进制数分为一组并代之以等值的十六进制数，小数部分从高位到低位每4位数分为一组并代之以等值的十六进制数，即可得到对应的十六进制数。例如：

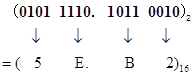
②十六进制转二进制：将十六进制数的每一位用等值的4位二进制数代替即可。例如：

（4）二进制与八进制之间的相互转化：

将二进制数转换为八进制数时，只要将二进制数的整数部分从低位到高位每3位分为一组并代之以等值的八进制数，同时将小数部分从高位到低位每3位分为一组并代之以等值的八进制数。在方法上与二-十六转换和十六-二转换的方法基本相同。例如：

二→八转换

八→二转换

三、二进制数的算术运算

1无符号二进制数的算术运算

（1）二进制加法

无符号二进制数的加法规则：

方框中的1为进位数。

（2）二进制减法

无符号二进制数的减法规则：

方框中的1为借位数。

（3）乘法运算和除法运算

①乘法运算是由左移被乘数和加法运算组成的。

②除法运算是由右移被除数和减法运算组成的。

2带符号二进制数的减法运算

负数的运算需要用有符号的二进制数表示。在定点运算的情况下，二进制数的最高位表示符号位，其中，0表示正数，1表示负数，其余部分为数值位。

将负数用补码表示，以便将减法运算变为加法运算。

（1）原码、反码、补码之间的转换见表1-1-7

表1-1-7　原码、反码、补码之间的转换

对于n位带符号的二进制数的原码、反码和补码的数值范围分别为：

原码：

反码：

补码：

（2）二进制补码的减法运算

二进制数减法运算的原理是减去一个正数相当于加上一个负数，即A－B＝A＋（－B），对（－B）求补码，然后进行加法运算。

二进制补码的加法运算应注意被加数补码与加数补码的位数相等，即让两个二进制数补码的符号位对齐。

乘法和除法可以采用移位和加法或减法的组合完成。

（3）溢出

当运算结果超出了数值位表示的范围时就会产生溢出。

解决办法：进行位扩展

溢出的判断：当最高位的进位与和数的符号位相反时，运算结果是错误的，产生溢出。

四、二进制代码

1各种二进制代码（见表1-1-8）

表1-1-8　各种二进制代码

2二进制码与格雷码的相互转化

（1）二进制码转格雷码

①格雷码的最高位（最左位）与二进制码的最高位相同。

②从左到右，逐一将二进制码相邻的2位相加（舍去进位），作为格雷码的下一位。

（2）格雷码转二进制码

①二进制码的最高位（最左位）与格雷码的最高位相同。

②将产生的每一位二进制码，与下一位相邻的格雷码相加（舍去进位），作为二进制码的下一位。

五、二值逻辑变量与基本逻辑运算

当0和1表示逻辑状态时，两个二进制数码按照某种指定的因果关系进行的运算称为逻辑运算。各种逻辑运算的类型见表1-1-9。

表1-1-9　逻辑运算总结

六、逻辑函数及其表示方法

1逻辑函数的几种表示方法（见表1-1-10）

表1-1-10　逻辑函数的几种表示方法

上述四种不同的表示方法所描述的是同一逻辑函数，因此它们之间有着必然的联系，可以从一种表示方法，得到其他表示方法。

2逻辑函数表示方法之间的转换

（1）真值表到逻辑图的转换

转换步骤：①根据真值表写出逻辑表达式；②用公式法或卡诺图法化简得到简化的逻辑表达式；③根据逻辑表达式画逻辑图。

（2）逻辑图到真值表的转换

转化步骤：①从逻辑图的输入端到输出端，逐级写出每个逻辑符号输出端的表达式，直到写出最后的输出变量的逻辑表达式；②化简变换，求简化的逻辑表达式；③将输入变量可能的取值逐个带入表达式进行计算，并将结果列表，即得真值表。

获取方式：扫码关注下面公众号，关注后

回复关键词【北京大学电子信息基础】或【北京大学电子信息基础】