2.1 试求图2-2-1所示的各杆1-1、2-2、3-3截面上的轴力,并作轴力图。
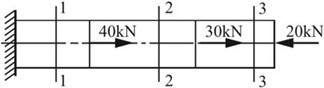
图2-2-1(a)
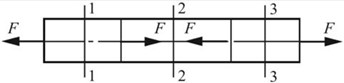
图2-2-1(b)
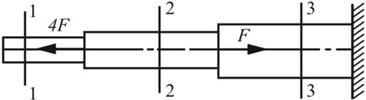
图2-2-1(c)
解:由截面法求得各截面上的轴力。由受拉为正,受压为负可得:
(a)FN1=50kN,FN2=10kN,FN3=-20kN;
(b)FN1=F,FN2=0,FN3=F;
(c)FN1=0,FN2=4F,FN3=3F。
对应的轴力图如图2-2-2所示。
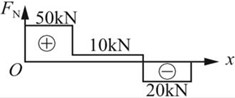
图2-2-2(a)
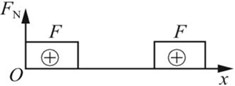
图2-2-2(b)
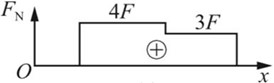
图2-2-2(c)
2.2 作用于图2-2-3所示零件上的拉力F=38kN,试问零件内最大拉应力发生于哪个截面上?并求其值。
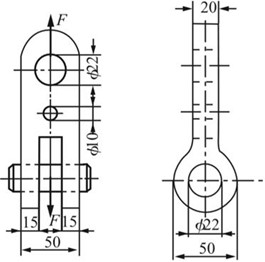
图2-2-3
解:由拉应力计算公式σ=F/A可知,轴力一定时,最大拉应力发生在横截面积最小截面上,如图2-2-4所示。
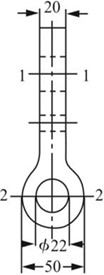
图2-2-4
1-1截面的面积:A1=(50-22)×20mm2=560mm2
2-2截面的面积:A2=(15+15)×(50-22)mm2=840mm2
比较可知,最大拉应力发生在1-1截面,且σmax=F/A1=38×103/(560×10-6)Pa=67.86MPa。
2.3 在图2-2-1(c),若1-1、2-2、3-3三个横截面的直径分别为:d1=15mm,d2=20mm,d3=24mm,F=8kN,试用图线表示横截面上的应力沿轴线的变化情况。
解:由题2.1可知,三截面上的轴力分别为:FN1=0,FN2=4F,FN3=3F。
则三个截面上的应力分别为
σ1=FN1/A1=0
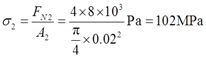
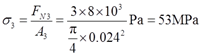
故横截面上应力沿轴线分布如图2-2-5所示。
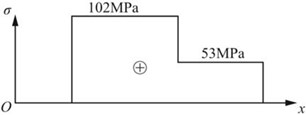
图2-2-5
2.4 在图2-2-6所示结构中,若钢拉杆BC的横截面直径为10mm,试求拉杆横截面上的应力。设由BC连接的1和2两部分均为刚体。
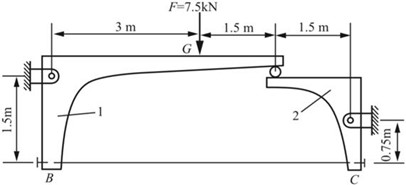
图2-2-6
解:将结构在节点A处断开,分别对两部分进行受力分析,如图2-2-7所示。
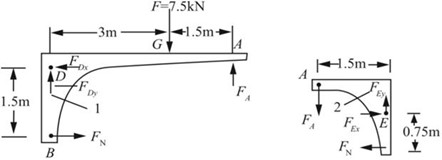
图2-2-7
根据平衡条件可得
∑MD=0,FN×1.5+FA×4.5-F×3=0
∑ME=0,FA×1.5-FN×0.75=0
则BC杆的轴力为:FN=6kN。
故拉杆BC的应力为:
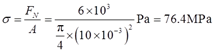
2.5 图2-2-8所示结构中,设两根横梁皆为刚体。1,2两杆的横截面直径分别为10mm和20mm。试求两杆横截面上的应力。
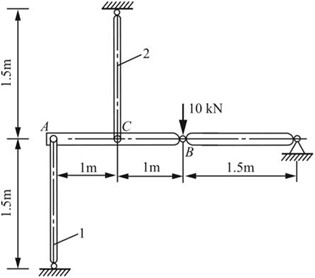
图2-2-8
解:对刚性横梁AB进行受力分析,如图2-2-9所示。
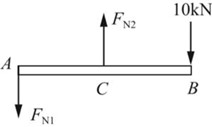
图2-2-9
静力平衡方程
∑Fy=0,FN2-FN1-10kN=0
∑Mc=0,FN1·1m-10kN·1m=0
解得:FN1=10kN,FN1=20kN。
故1、2两杆的应力分别为
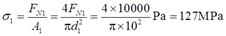
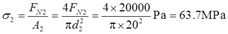
2.6 直径为10mm的圆杆,在拉力F=10kN的作用下,试求斜截面上的最大切应力,并求与横截面夹角为α=30°的斜截面上正应力及切应力。
解:由轴向拉压变形杆中斜截面的应力计算公式σα=FNcos2α/A,τα=FNsin2α/(2A)可知,在α=45°时,杆内该斜截面上的切应力达到最大值为
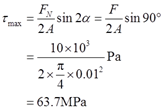
且α=30°的斜截面上的应力为
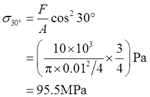
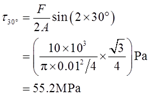
2.7 如图2-2-10所示,油缸盖与缸体采用6个螺栓连接。已知油缸内径D=350mm,油压p=1MPa。若螺栓材料的许用应力[σ]=40MPa,试确定螺栓的内径。
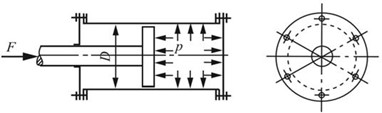
图2-2-10
解:对油缸盖进行受力分析。
假设每个螺栓平均受力,则由平衡条件可得6个螺栓所承受的总的轴力为
F=pA=p×πD2/4=6FN
其中,每个螺栓受到的轴向力为:FN=pπD2/24。
由强度条件可得
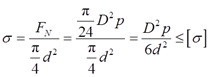
即有螺栓内径满足
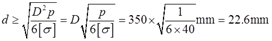
2.8 汽车离合器踏板如图2-2-11所示。已知踏板受到压力F1=400N作用,拉杆1的直径d=9mm,杠杆臂长L=330mm,l=56mm,若拉杆的许用应力[σ]=50MPa,试校核拉杆1的强度。
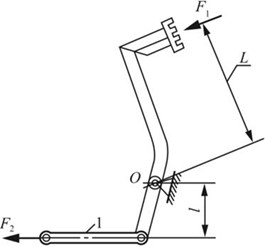
图2-2-11
解:如图2-2-11所示,由平衡条件可得
∑MO=0,F1L-F2l=0
则拉杆1的轴力为
FN=F2=F1L/l=400×0.33/0.056N=2357N
拉杆1的工作应力为
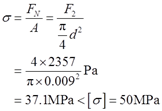
故拉杆1满足强度要求。
2.9 冷辙机的曲柄滑块机构如图2-2-12所示。镦压工件时连杆接近水平位置,承受的镦压力F=1100kN。连杆是矩形截面,高度h与宽度b之比为h/b=1.4。材料为45钢,许用应力[σ]=58MPa,试确定截面尺寸h及b。
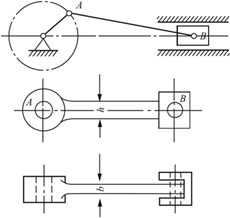
图2-2-12
解:根据正应力强度条件,连杆接近水平位置时,有
σ=F/A=F/(bh)≤[σ]
其中,h/b=1.4。
则有:
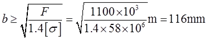
可得:h=1.4b≥1.4×116=162mm。
因此,截面尺寸满足:b≥116mm,h≥162mm。
2.10 图2-2-13所示的双杠杆夹紧机构,需产生一对20kN的夹紧力,已知该三杆的材料相同,[σ]=100MPa,α=30°。试求水平杆AB及两斜杆BC和BD的横截面直径。
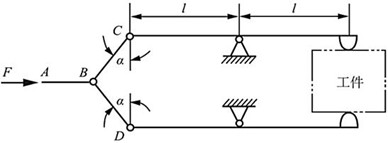
图2-2-13
解:杆AB、杆BC、杆BD均为二力杆。
如图2-2-14(a)所示,以CE杆为研究对象。
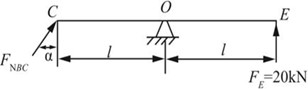
图2-2-14(a)
由平衡条件得:FNBClcosα-FEl=0。
则BC杆轴力:FNBC=FE/cosα=20kN/cos30°=23.1kN。
根据BC杆强度条件:σBC=FNBC/ABC=4FNBC/(πdBC2)≤[σ]。
可得BC杆直径:
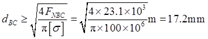
由结构对称性可知,BD杆直径满足:dBD≥17.2mm。
如图2-2-14(b)所示,对节点B进行受力分析。
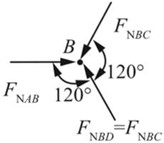
图2-2-14(b)
由平衡条件得:FNAB=FNBC=23.1kN。
同理,根据AB杆强度条件可得该杆直径满足:dAB≥17.2mm。
2.11 如图2-2-15所示,卧式拉床的油缸内径D=186mm,活塞杆直径d1=65mm,材料为20Cr并经过热处理,[σ]杆=130MPa。缸盖由6个M20的螺栓与缸体连接,M20螺栓的内径d=17.3mm,材料为35钢,经热处理后[σ]螺=110MPa。试按活塞杆和螺栓强度确定最大油压p。
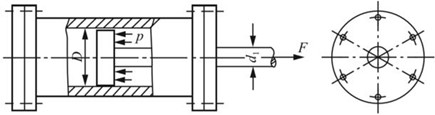
图2-2-15
解:(1)按活塞杆强度要求确定最大油压
分析活塞杆受力可得其在油压力作用下的轴力为:F1=p·π(D2-d12)/4。
由活塞杆强度条件:σ1=F1/A杆=p1(D2-d12)/d12≤[σ]杆。
可得油压满足:
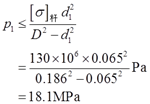
(2)根据螺栓强度要求确定油压
对缸盖进行受力分析,由平衡条件6F2=p·π(D2-d12)/4得每个螺栓承受的轴力为
F2=p·π(D2-d12)/24
由螺栓的强度条件:σ2=F2/A螺=p2(D2-d12)/6d2≤[σ]螺。
可得油压满足:
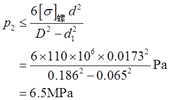
综上,取较小值,最大油压为:pmax=6.5MPa。
2.12 在图2-2-16所示简易吊车中,BC为钢杆,AB为木杆。木杆AB的横截面面积A1=10000mm2时,许用应力[σ]1=7MPa;钢杆BC的横截面面积A2=600mm2,许用拉应力[σ]2=160MPa。试求许可吊重F。
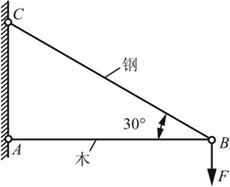
图2-2-16
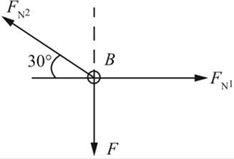
图2-2-17
解:分析节点B处受力,如图2-2-17所示,由平衡条件
∑Fx=0,FN1-FN2cos30°=0
∑Fy=0,FN2sin30°-F=0
可得两杆轴力:
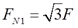
FN2=2F。
(1)按木杆的强度要求确定许可吊重
由木杆强度条件σ1=FN1/A1≤[σ]1,可得
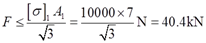
(2)按钢杆的强度要求确定许可吊重
由钢杆强度条件σ2=FN2/A2≤[σ]2,可得F≤[σ]2A2/2=(1/2)×600×160N=48kN。
综上,取较小值,许可吊重[F]=40.4kN。
2.13 某拉伸试验机的结构示意图如图2-2-18所示。设试验机的CD杆与试件AB的材料同为低碳钢,其σp=200MPa,σs=240MPa,σb=400MPa。试验机最大拉力为100kN。
(1)用这一试验机作拉断试验时,试样直径最大可达多大?
(2)若设计时取试验机的安全因数n=2,则CD杆的横截面面积为多少?
(3)若试样直径d=10mm,今欲测弹性模量E,则所加载荷最大不能超过多少?
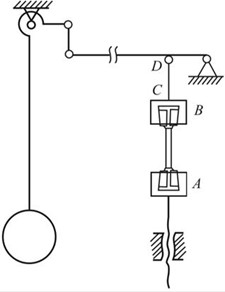
图2-2-18
解:(1)利用塑性材料拉断条件,材料被拉断的最小应力为
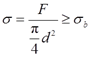
则试件的直径
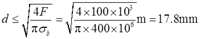
(2)CD杆的强度条件:σ=F/A≤[σ]=σs/n。
则杆的横截面面积为:A≥nF/σs=2×100×103/(240×106)m2=833mm2。
(3)测弹性模量时,试件的最大应力不应超过其弹性极限σp,即
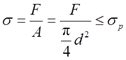
解得:F≤σpπd2/4=[200×106×(π/4)×0.012]N=15.7kN。
2.14 某铣床工作台进给油缸如图2-2-19所示,缸内工作油压p=2MPa,油缸内径D=75mm,活塞杆直径d=18mm。已知活塞杆材料的许用应力[σ]=50MPa,试校核活塞杆的强度。
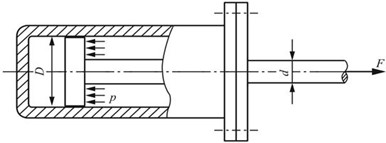
图2-2-19
解:分析活塞杆受力可得,其在油压力作用下活塞杆的轴力为
F=p(π/4)(D2-d2)
则活塞杆的工作应力为
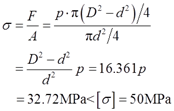
所以活塞杆满足强度要求。
2.15 图2-2-20所示的拉杆沿斜截面m-m由两部分胶合而成。设在胶合面上许用拉应力[σ]=100MPa,许用切应力[τ]=50MPa。并设杆件的拉力由胶合面的强度控制。试问:为使杆件承受最大拉力F,α角的值应为多少?若杆件横截面面积为400mm2,并规定α≤60°,试确定许可载荷F。
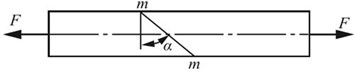
图2-2-20
解:当正应力和切应力同时达到各自的许用应力时,拉力F达到最大值,并由直杆轴向拉伸时斜截面上的应力公式可得
σα=Fcos2α/A=[σ],τα=Fsinαcosα/A=[τ]
联立以上二式,可得:tanα=[τ]/[σ]=50/100=0.5,即α=26.6°。
故此时杆件可承受拉力最大,值为
Fmax=A[σ]/cos2α=400×100/cos226.6°N=50kN
2.16 在压力F作用下的杆件如图2-2-21(a)所示,如再考虑其自重影响,并要求任一横截面的应力皆等于许用应力[σ]。试确定横截面面积沿轴线的变化规律,并计算杆件变形。设材料的密度为ρ。
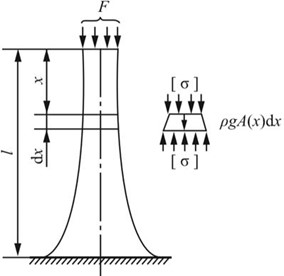
图2-2-21(a)
解:如图2-2-21(a)所示,由平衡方程∑Fx=0,有
[σ]A(x)+ρgA(x)dx-[σ][A(x)+dA(x)]=0
得出
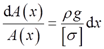
等号两边积分
lnA(x)=ρgx/[σ]+C①
确定积分常数的边界条件是,当x=0时,A(x)=A0=F/[σ]②
把以上边界条件代入式①,得C=lnA0。
这样,式①化为
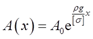 ③
③
这就是A(x)沿轴线的变化规律。
因为等强度杆在任一横截面上的应力都等于常量,则有
|ε|=[σ]/E=常量
于是整个杆件的总变形是
|Δl|=|εl|=-[σ]l/E
实际中,式③所示的形状加工时非常困难的。所以工程上通常采用阶梯形杆或锥台形杆,如图2-2-21(b)(c)所示。
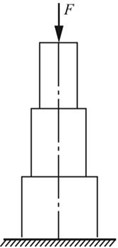
图2-2-21(b)
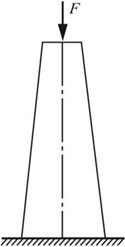
图2-2-21(c)
2.17 在图2-2-22所示杆系中,BC和BD两杆的材料相同,且抗拉和抗压许用应力也相同,同为[σ]。为使杆系使用的材料最省,试求夹角θ的值。
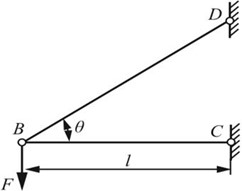
图2-2-22
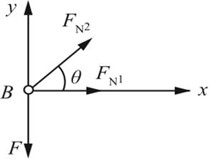
图2-2-23
解:如图2-2-23所示,对节点B进行受力分析,根据平衡条件
∑Fx=0,FN2cosθ+FN1=0
∑Fy=0,FN2sinθ-F=0
可得两杆轴力:FN1=-Fcotθ(压力),FN2=F/sinθ(拉力)。
由两杆的强度条件:σ1=FN1/A1≤[σ],σ2=FN2/A2≤[σ]。
可知两杆同时达到许用应力时的横截面面积最为合理,即
A1≥(Fcotθ)/[σ],A2≥F/([σ]sinθ)
此时结构的体积
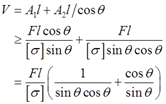
令dV/dθ=0,可得体积最小时两杆的夹角满足:tan2θ=2。
即
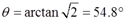
2.18 阶梯形直杆如图2-2-24所示。已知:A1=800mm2,A2=400mm2,E=200GPa。求杆的总伸长Δl。
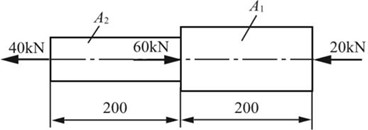
图2-2-24
解:由截面法可得杆各段轴力:FN1=-20kN,FN2=40kN。
由胡克定律可得杆的总伸长
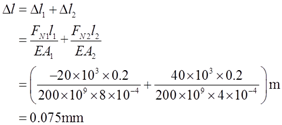
2.19 为了改进万吨水压机的设计,在四根立柱的小型水压机上进行模型实验,测得立柱的总伸长Δl=0.4mm。立柱直径d=80mm,长度l=1350mm。材料的E=210GPa。问每一立柱受到的轴向力有多大?水压机的中心载荷F等于多少?
解:由题意可知,四根立柱平均承担水压机的中心载荷,并产生相同的变形量。
由拉压胡克定律Δl=FNl/(EA),可得每个立柱受到的轴向力为
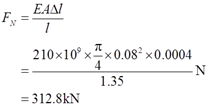
则水压机的中心载荷为:F=4FN=4×312.8kN=1251.2kN。
2.20 如图2-2-25所示,设CG为刚体(即CG的弯曲变形可以忽略),BC为铜杆,DG为钢杆,两杆的横截面面积分别为A1和A2,弹性模量分别为E1和E2。如要求CG始终保持水平位置,试求力的作用位置x。
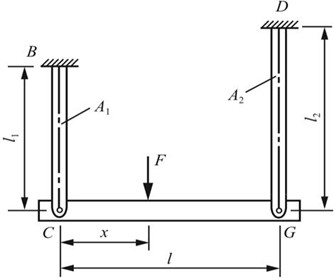
图2-2-25
解:对CG杆进行受力分析,如图2-2-26所示。
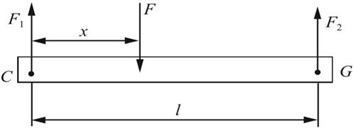
图2-2-26
根据平衡条件:∑Mc=0,F2l-Fx=0,∑Fy=0,F1+F2-F=0。
可得两杆的轴力:F1=F(l-x)/l,F2=xF/l。
则由胡可定律可得两杆伸长量
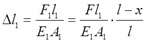
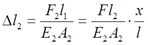
要使得CG杆保持水平,应有协调条件:Δl1=Δl2,即
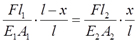
解得:
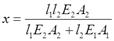
*2.21 如图2-2-27所示,BC、BD两杆原在水平位置。在F力作用下,两杆发生变形,在B点的竖直位移为Δ。若两杆的抗拉刚度同为EA,试求Δ与F的关系。(提示:计算时应考虑BC和BD的角度变化,即变形后两杆不再保持水平。)
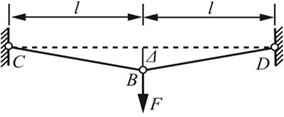
图2-2-27
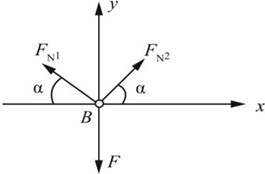
图2-2-28
解:对节点B进行受力分析,如图2-2-28所示,根据平衡条件
∑Fx=0,FN2cosα-FN1cosα=0
∑Fy=0,(FN1+FN2)sinα-F=0
可得两杆轴力:FN1=FN2=F/(2sinα)。
变形后,由于α角度非常小,近似有
sinα=Δ/(l+Δl)=tanα=Δ/l
其中由胡克定律可知杆的变形
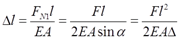 ①
①
又由几何关系可得
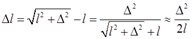 ②
②
联立式①②可得:Δ3=Fl3/(EA)。
即载荷F和位移Δ之间的关系:
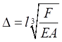
2.22 如图2-2-29所示,像矿山升降机钢缆这类很长的拉杆,分析强度和变形时应考虑其自重的影响。设材料的密度为ρ,许用应力为[σ]。钢缆下端所受拉为F,钢缆截面不变。试求钢缆的允许长度及其总伸长。
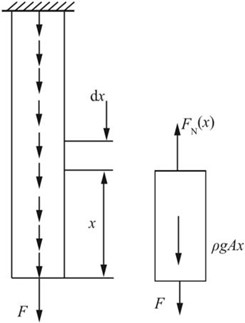
图2-2-29
解:建立如图2-2-29所示坐标系,并取x截面以下部分进行受力分析。
钢缆x截面的轴力:FN(x)=F+ρgAx。
由此可知最大轴力发生在固定端截面,其值为:FN=F+ρgAL。
根据强度条件有:σ=FN/A=(F+ρgAL)/A≤[σ]。
可得钢缆允许长:L≤(A[σ]-F)/(ρgA)。
故由胡克定律可得钢缆总伸长
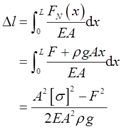
2.23 铸铁柱尺寸如图2-2-30所示,轴向压力F=30kN,E=120GPa。若不计自重,试求柱的变形。
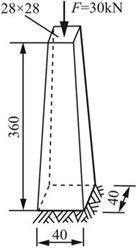
图2-2-30
解:距离柱底x处横截面面积为:A(x)=(40-x/30)2。
根据胡克定律可得柱的变形量
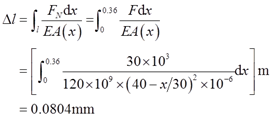
即柱缩短了0.0804mm。
2.24 图2-2-31中AD和BE两根铸铁柱的形状和尺寸与题2.23中的铸铁柱相同。若设横梁AB为刚体,F=50kN,试求F作用点C的铅垂位移。
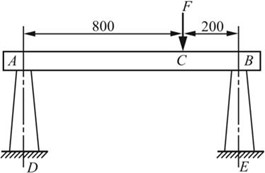
图2-2-31
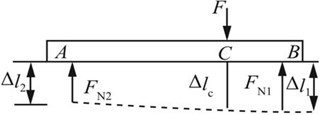
图2-2-32
解:对杆AB进行受力分析,其力和位移图如图2-2-32所示。根据平衡条件
∑Fy=0,FN1+FN2-F=0
∑MA=0,FN1×1000-F×800=0
可得BE、AD杆的轴力为:FN1=40kN,FN2=10kN。
由胡克定律
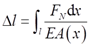
其中A(x)=(40-x/30)2。
可得两杆的变形量
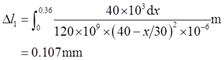
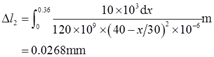
由图2-2-32所示几何关系可得C点位移
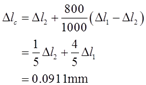
*2.25 图2-2-33(a)所示的简单杆系,其两杆的长度均为l=3m,横截面面积A=1000mm2。材料的应力一应变关系如图2-2-33(b)所示。E1=70GPa,E2=10GPa。试分别计算当F=80kN和F=120kN时,节点B的铅垂位移。
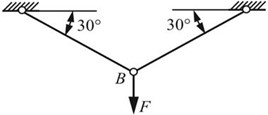
图2-2-33(a)
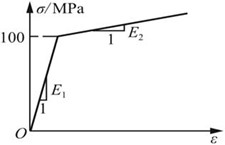
图2-2-33(b)
解:根据结构和载荷对称性可知两杆内力相等,且FN1=FN2=FN=F。
(1)F=80kN时,杆内横截面上正应力
σ=FN/A=F/A=80×103/(1000×10-6)Pa=80MPa<100MPa
由图2-2-33(b)可知,两杆伸长量均为Δl=FNl/(EA),其中E=E1。
形后几何关系如图2-2-34所示。
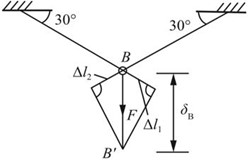
图2-2-34
可得B点位移
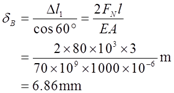
(2)F=120kN时,杆内横截面上正应力
σ=FN/A=F/A=120×103/(1000×10-6)Pa=120MPa>100MPa
因此,变形要分两段进行计算。又变形是在弹性变形范围内产生的,故可以用叠加法将两段杆的变形叠加,当应力为100MPa时,对应的拉力F=σA=100×1000=100kN。因此前一段的拉力为100kN,后一段的拉力为20kN。则根据几何关系可得B点位移
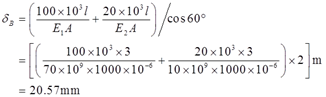
2.26 如图2-2-35所示,打入粘土的木桩长为L,顶上载荷为F。设载荷全由摩擦力来承担,且沿木桩单位长度内的摩擦力f按抛物线f=Ky2变化,这里K为常数,y是截面距木桩底部的距离。若F=420kN,L=12m,A=64000mm2,E=10GPa.试确定常数K,并求木桩的缩短量。
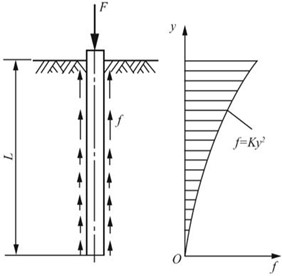
图2-2-35
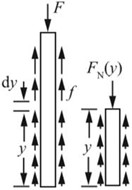
图2-2-36
解:木桩受力分析如图2-2-36所示。根据平衡条件
∑Fy=0,
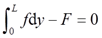
将f=Ky2代入即可确定常数K:K=3F/L3=3×420×103/123N/m3=729N/m3。
在距离下端y处截面上的轴力为
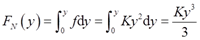
则由胡克定律可得木桩总的变形量
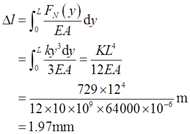
即木桩缩短了1.97mm。
2.27 抗拉(压)刚度为EA的等直杆,受力情况如图2-2-37所示。试问:
(1)总伸长是否为Δl=F1l1/(EA)+F2l2/(EA)?如有错误,正确的算式是什么?
(2)应变能否为Vε=F12l1/(2EA)+F22l2/(2EA)?如有错误,正确的算式是什么?
(3)若l1=l2=l,F1+F2=F(常量),试求Vεmax、Vεmin,并求两种情况下的比值F2/F1。
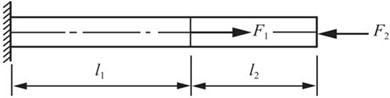
图2-2-37
解:(1)不是。正确的算法为:Δl=l1(F1-F2)/(EA)-F2l2/(EA)。
(2)不是。正确的算法为:
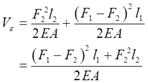
(3)将l1=l2=l,F1=F2=F代入(2)所得到的式中,可得轴的应变能
Vε=l(F2+5F22-4FF2)/(2EA)
令dVε/dF2=0,可得应变能的极值点,此时F2=2F/5,且有
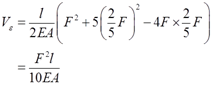
在边界点F1=0,F2=F处,有Vε=F2l/(EA);
在边界点F2=0,F1=F处,有Vε=F2l/(2EA)。
应变能时关于F2的二次函数,所以应变能的最大值为Vεmax=F2l/(EA),此时F2/F1→∞。
最小应变能:Vεmin=F2l/(10EA),此时F2/F1=3/2。
2.28 长度为l的杆件,抗拉刚度为EA。若在杆件两端沿轴线先作用拉力F1,再作用F2,在作用F2的过程中,变形能的增量是否为ΔVε=F22l/(2EA)?
解:变形能的增量不是ΔVε=F22l/(2EA)。
在F1单独作用下杆的应变能:Vε1=F12l/(2EA)。
在弹性小变形范围内,变形能的大小与加载顺序无关,则先加载F1再加载F2后,杆件的应变能:Vε2=(F1+F2)2l/(2EA)。
由此可得应变能的增量为
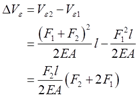
2.29 如图2-2-38所示,设横梁ABCD为刚体。横截面面积为76.36mm2的钢索绕过无摩擦的滑轮。设F=20kN,钢索的E=177GPa。试求钢索内的应力和C点的铅垂位移。
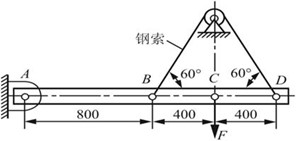
图2-2-38
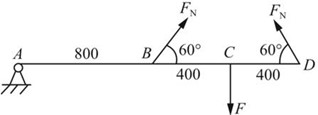
图2-2-39
解:对AD梁进行受力分析,如图2-2-39所示。
根据平衡方程
∑MA=0,FNsin60°×800+FNsin60°×1600-F×1200=0
可得钢索承受的拉力:
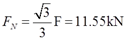
故钢索内的应力:σ=FN/A=11.55×103/(76.36×10-6)Pa=151MPa。
钢索的变形能:
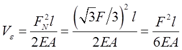
根据题意,钢索长:l=400mm×2×2=1600mm=1.6m。
利用功能原理,钢索的变形能等于力F做功,即WC=Vε,故FΔC/2=F2l/(6EA)。
则在力F作用下C点位移
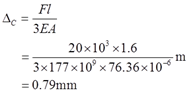
2.30 钢制受拉杆件如图2-2-40所示,横截面面积A=200mm2,l=5m,密度为7.8×103kg/m3,设E=200GPa。如不计自重,试计算杆件的应变能Vε和应变能密度νε。如考虑自重影响,试计算杆件的应变能,并求应变能密度的最大值。
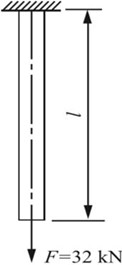
图2-2-40
解:(1)不计自重时,杆件应变能
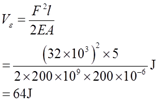
应变能密度
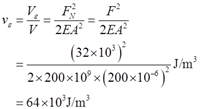
(2)考虑自重时,在距离底部为x处横截面上的轴力:FN(x)=F+ρAgx。
此时杆件应变能
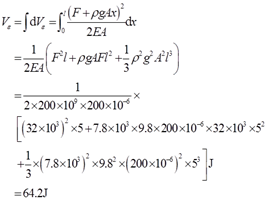
应变能密度
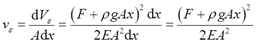
即在x=l时,应变能密度取得最大值,为
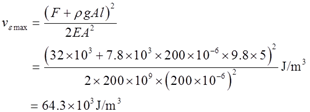
2.31 在图2-2-41所示简单杆系中,设AB和AC分别为直径是20mm和24mm的圆截面杆,E=200GPa,F=5kN。试求A点的铅垂位移。
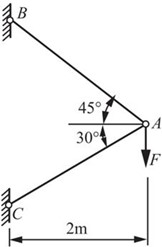
图2-2-41
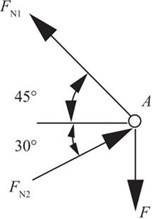
图2-2-42
解:对节点A进行受力分析,如图2-2-42所示。
根据平衡条件
∑Fx=0,-FN1cos45°+FN2cos30°=0
∑Fy=0,FN1sin45°+FN2sin30°-F=0
可得各杆轴力:FN1=0.897F,FN2=0.732F。
则该杆系总的应变能:
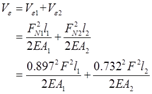
其中根据图中几何关系可知各杆长:
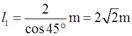
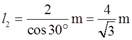
根据功能原理Vε=W=FδA/2,可得A点铅垂位移
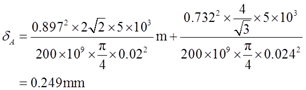
2.32 由五根钢杆组成的杆系如图2-2-43所示。各杆横截面面积均为500mm2,E=200GPa。设沿对角线AC方向作用一对20kN的力,试求A、C两点的距离改变。
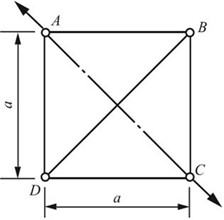
图2-2-43
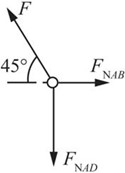
图2-2-44
解:分析节点A受力,如图2-2-44所示。
根据平衡条件及其结构和载荷的对称性可知
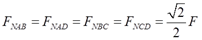
FNBD=-F
则该杆系总的应变能为:
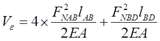
根据功能原理有Vε=FΔAC/2,则A、C两点的距离改变量为
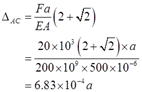
2.33 如图2-2-45所示,截面分别为圆形和正方形的两种薄壁杆件,作用轴向拉力F。若材料的弹性模量为E,泊松比为μ,试分别确定横截面上AB两点的距离改变量δAB。
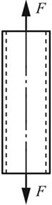
图2-2-45(a)
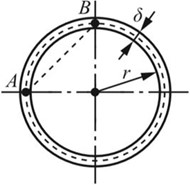
图2-2-45(b)
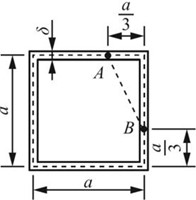
图2-2-45(c)
解:(1)圆截面
轴向线应变为ε=F/(EA)=F/(Eπdδ),由于泊松效应,横向线应变为
ε′=-με=-μF/(Eπdδ)
横向线应变也可表示为ε′=Δd/d,所以
Δd/d=-μF/(Eπdδ)
Δd=-μF/(Eπδ)
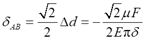
(2)正方形截面
横向线应变为ε=F/(EA)=F/(4Eaδ),由于泊松效应,横向线应变为
ε′=-με=-μF/(4Eaδ)
横向线应变也可表示为ε′=Δa/a,所以
Δa/a=-μF/(4Eaδ)
Δa=-μF/(4Eδ)
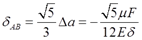
2.34 在图2-2-46所示支架中,设拉杆DE的长为2m,横截面的直径为15mm的圆形,E=210GPa。若ADB和AEC两杆可以看作是刚体,F=20kN,试求F力作用点A的铅垂位移和C点的水平位移。
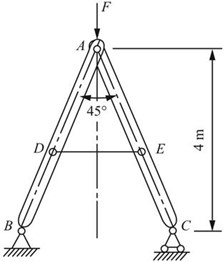
图2-2-46
解:如图2-2-47所示,对整体进行分析。
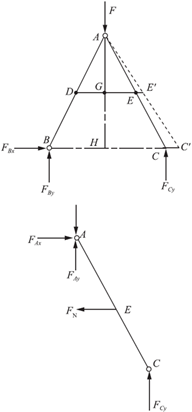
图2-2-47
根据平衡条件可得:∑MB=0,FCy=0.5F。
对AC杆进行受力分析,可得平衡条件
∑MA=0,
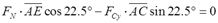
解得:
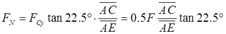
根据几何关系可得:
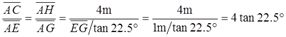
故杆DE的轴力:FN=2Ftan222.5°。
该杆系总的应变能:
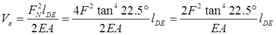
根据功能原理FΔA/2=Vε可得,点A铅垂位移
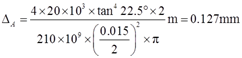
根据胡克定律可得DE杆的变形量
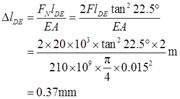
又根据图2-2-47中所示变形后几何关系得到
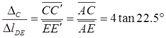
故C点水平位移:ΔC=ΔlDE·4tan22.5°=0.37×4tan22.5°mm=0.613mm。
2.35 图2-2-48所示结构中,ABC为刚体,拉杆CD的拉压刚度为EA,长度为l,在A点作用铅垂方向的集中力F。试求A点的铅垂位移。
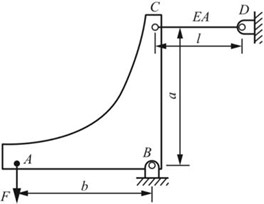
图2-2-48
解:对B点取矩,∑MB=0,Fb-FCDa=0。
拉杆CD的拉力为FCD=Fb/a。
伸长量Δl=FCDl/(EA)=Fbl/(EAa)。
即点C向左运动ΔC=Fbl/(EAa)。
ABC为刚体,所以有
ΔC/a=ΔA/b⇒Fbl/(EAa2)=ΔA/b
所以ΔA=Fb2l/(EAa2)(↓)。
2.36 图2-2-49所示简易支架中,AB为刚性杆,拉杆CD的拉压刚度为EA。试求B点的铅垂位移。
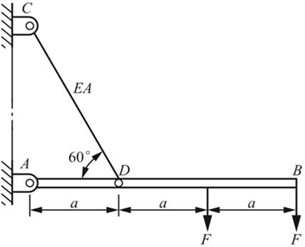
图2-2-49
解:对A点取矩,∑MA=0,F·2a+F·3a-FCDasin60°=0。
所以拉杆CD的拉力为
FCD=5F/sin60°
CD杆的伸长量为
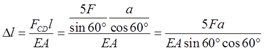
由变形协调关系,如图2-2-50,则D点的铅垂位移为
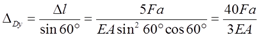
ΔBy=3ΔDy=40Fa/EA
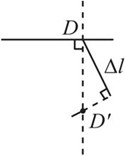
图2-2-50
2.37 试用能量法求例2.9中简易起重机B点的水平位移,如图2-2-51所示。
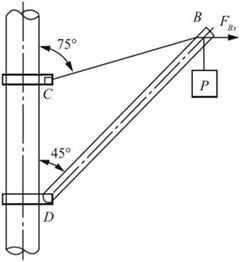
图2-2-51
解:以δBy和δBx表示B点的铅垂和水平位移,FN1和FN2表示钢索BC和钢杆BD的轴力,WP表示P力完成的功。在教材例2.9中,根据外力做工等于杆系应变能的原则,可求得
WP=PδBy/2=FN12l1/(2E1A1)+FN22l/(2EA)①
设想在作用P之前,BC和BD因FBx引起的轴力分别是
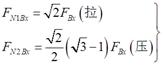 ②
②
WBx表示FBx作的功,则有
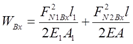 ③
③
发生位移δBx的过程中,FBx的大小不变。则有外力作功为
W=WBx+WP+FBxδBx
由题意可知,两根构件的轴力分别是(FN1+FN1Bx)和(FN2+FN2Bx),因而
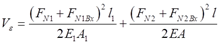
令W=Vε,得
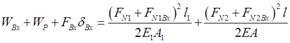
从上式中减去式①和式③两式,得
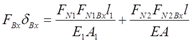
将式②中的FN1Bx和FN2Bx代入,得
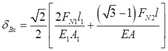
将教材例2.9中的具体数值代入上式,可得:δBx=2.78×10-3m。
*2.38 如图2-2-52所示简单桁架的三根杆件均为钢材制成,横截面面积均为300mm2时,E=200GPa。若F=5kN,试求C点的水平及铅垂位移。
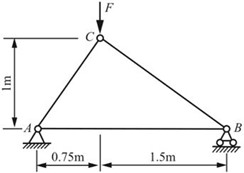
图2-2-52
解:由平衡条件
∑MA=0,FB×2.25-F×0.75=0
解得
FB=F/3
C铰链的受力图如图2-2-53(a)所示。
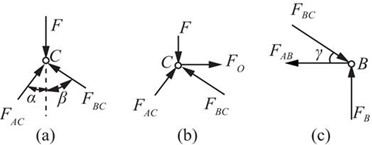
图2-2-53
α和β角可由图2-2-52的几何关系确定
cosα=1/1.25,α=36.9°
cosβ=1/1.8,β=56.3°
由平衡条件
∑Fy=0,FACcosα+FBCcosβ-F=0
∑Fx=0,FACsinα-FBCsinβ=0
解得
FAC=0.83F,FBC=0.6F
B铰链的受力图如图2-2-53(c)所示,由平衡条件
∑Fx=0,FAB-FBCcosγ=0
将
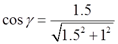
代入上式,解得
FAB=0.5F
杆系的总变形能为
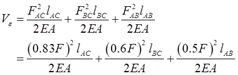
(1)C点垂直位移
应用Vε=FδYC/2,C点的垂直位移为
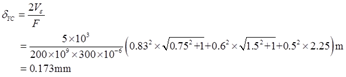
(2)C点水平位移
C点无水平力作用,欲求C点的水平位移,则必须在C点加上一水平方向的虚载荷F0,C点的受力图如2-2-53(b)所示,由平衡条件
∑Fy=0,FACcosα+FBCcosβ-F=0
∑Fx=0,FACsinα-FBCsinβ+F0=0
解得
FAC=0.83F-0.56F0
FBC=0.6F+0.8F0
B铰链的受力图如2-2-53(c)所示,由平衡条件
∑Fx=0,FAB-FBCcosγ=0
解得
FAB=0.5F+0.66F0
杆系的总变形能为
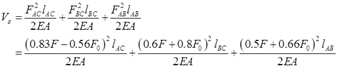
应用卡式定理,C点的水平位移为
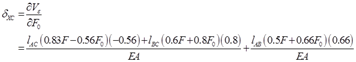
令F0=0,则
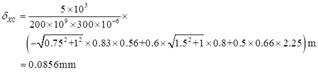
2.39 木制短柱的四个角用四个40mm×40mm×4mm的等边角钢加固,如图2-2-54所示。已知角钢的许用应力[σ]钢=160MPa,E钢=200GPa;木材的许用应力[σ]木=12MPa,E木=10GPa。试求许可载荷F。
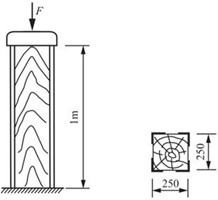
图2-2-54
解:由平衡条件可得:F钢+F木-F=0①
由几何关系可知角钢和木材的变形量相等,即有变形协调条件:Δl钢=Δl木。
又由胡克定律可得:Δl钢=F钢l/(E钢A钢),Δl木=F木l/(E木A木)。
其中,查型钢表知单个40mm×40mm×4mm角钢的横截面积:A钢=308.6mm2。
故有:
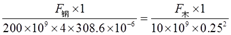 ②
②
联立式①②可得各自承受的轴力:F钢=0.283F,F木=0.717F。
根据角钢的强度条件:
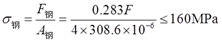
可得许可载荷:[F1]=698kN。
根据木材的强度条件:σ木=F木/A木=0.717F/0.252≤12MPa。
可得许可载荷:[F2]=1046kN。
综上,取较小值许可载荷F=698kN。
2.40 在两端固定的杆件的截面C上,沿轴线作用F力(图2-2-55(a))。试求两端的约束力。
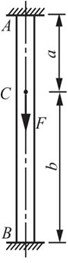
图2-2-55(a)
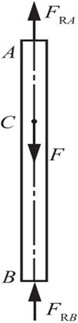
图2-2-55(b)
解:由图2-2-55(b)可得静力平衡方程:FRA+FRB-F=0。
杆两端固定,AB总长度没有改变,则受拉段AC与受压段BC的变形量相互抵消,即有变形协调方程:Δla+Δlb=0。
又由胡克定律可知:Δla=FRAa/(EA),Δlb=-FRBb/(EA)。
代入变形协调方程,并联立平衡方程可得两端约束力
FRA=Fb/(a+b)(↑),FRB=Fa/(a+b)(↑)
2.41 两根材料不同但截面尺寸相同的矩形截面杆件,同时固定连接于两端的刚性板上,且E1>E2,如图2-2-56所示。若使两杆都为均匀拉伸,试求拉力F的偏心距e。
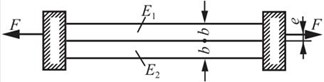
图2-2-56
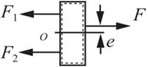
图2-2-57
解:如图2-2-57所示,由平衡条件可得
∑Fx=0,-F1-F2+F=0①
∑MO=0,(F1-F2)b/2-Fe=0②
由题中均匀拉伸可知变形协调条件:Δl1=Δl2。
在拉力作用下,由胡克定律可得:Δl1=F1l/(E1A1),Δl2=F2l/(E2A2)。
代入变形协调条件得:F1l/(E1A)=F2l/(E2A)③
联立式①②③可得偏心距:
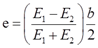
2.42 受预拉力10kN张紧缆索如图2-2-58所示。若在C点再作用向下的载荷15kN,并设缆索不能承受压力,试求在h=l/5和h=4l/5两种情况下,AC和BC两段内的内力。
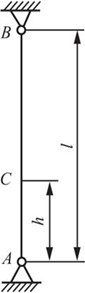
图2-2-58
解:在预拉力单独作用下,绳索内力F0=10kN。
在载荷F=15kN作用下,将缆索AB看作是细杆,其受力如图2-2-59所示。
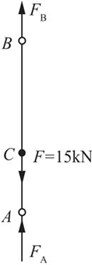
图2-2-59
由平衡条件可得:FA+FB-F=0。
变形协调条件:ΔlBC=ΔlAC。
由胡克定律可得协调方程变为:FB(l-h)/(EA)=FAh/(EA)。
解得:FA=F(l-h)/l,FB=Fh/l。
由叠加原理可得AC段和BC段的内力分别为
FAC=F0-FA=F0-F(l-h)/l①
FBC=F0+FB=F0+Fh/l②
由于钢索不承受压力,即有FAC=F0-F(l-h)/l=10-15(l-h)/h≥0,解得:h≥l/3。
故h=4l/5>l/3时,由式①②可得:FAC=7kN,FBC=22kN。
h=l/5<l/3时,力全由BC段承担,则有:FAC=0,FBC=15kN。
2.43 在图2-2-60所示结构中,假设AC梁为刚性杆,杆1,2,3横截面面积相等,材料相同。试求三杆的轴力。
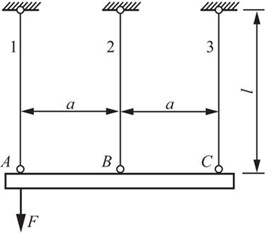
图2-2-60
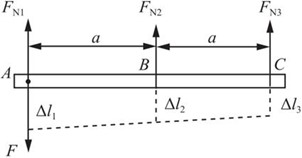
图2-2-61
解:对AC梁进行受力分析,并作出变形位移图,如图2-2-61所示。
由平衡条件可得
∑Fy=0,FN1+FN2+FN3-F=0①
∑MA=0,FN2·a+FN3·2a=0②
由图2-2-61中所示几何关系可得变形协调方程:Δl1+Δl3=2Δl2③
由胡克定律,式③可变形为:FN1l/(EA)+FN3l/(EA)=2FN2l/(EA)。
整理得:FN1+FN3=2FN2④
联立式①②④可得各杆轴力
FN1=5F/6,FN2=F/3,FN3=-F/6
2.44 如图2-2-62所示,刚性杆AB悬挂于1,2两杆上,1杆的横截面面积为60mm2,2杆为120mm2,且两杆材料相同。若F=6kN,试求两杆的轴力及支座A的约束力。
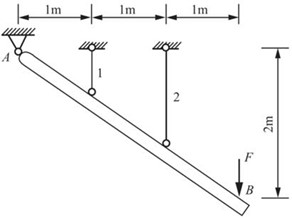
图2-2-62
解:对AB杆进行受力分析,并作出变形位移图,如图2-2-63所示。
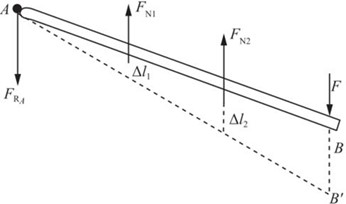
图2-2-63
由平衡条件可得
∑Fy=0,FN1+FN2-FRA-F=0①
∑MA=0,FN1×1+FN2×2-F×3=0②
由图2-2-63中所示几何关系可得变形协调方程:2Δl1=Δl2③
由胡克定律式③可变形为:2FN1l1/(EA1)=FN2l2/(EA2)。
将已知条件l2=2l1,A2=120mm2=2A1代入上式,可得
FN1=FN2/2④
联立式①②④可得各杆轴力及A处约束力
FN1=3.6kN,FN2=7.2kN,FRA=4.8kN
2.45 图2-2-64所示支架中的三根杆件材料相同,杆1的横截面面积为200mm2,杆2为300mm2,杆3为400mm2。若F=30kN,试求各杆横截面上的应力。
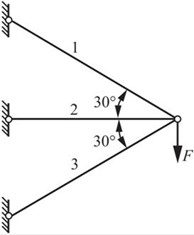
图2-2-64
解:对节点A进行受力分析,并作出变形位移图,如图2-2-65所示。
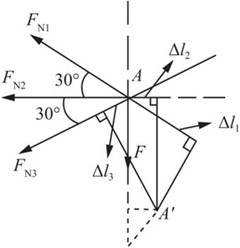
图2-2-65
由平衡条件可得
∑Fx=0,FN1cos30°+FN3cos30°+FN2=0①
∑Fy=0,FN1sin30°-FN3sin30°-F=0②
由图2-2-65中变形几何关系可得变形协调条件
Δl1/sin30°=2Δl2/tan30°+Δl3/sin30°③
由胡克定律式③可变形为
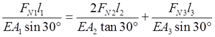 ④
④
联立式①②④可得各杆轴力
FN1=25.4kN,FN2=8.04kN,FN3=-34.6kN
故各杆内应力
σ1=FN1/A1=25.4×103/(200×10-6)Pa=127MPa
σ2=FN2/A2=8.04×103/(300×10-6)Pa=26.8MPa
σ3=FN3/A3=-34.6×103/(400×10-6)Pa=-86.5MPa
2.46 为了说明用螺栓将机器各部分紧固连接的问题,以图2-2-66所示在铸铁套筒内套钢螺栓的情况为例。若垫片贴住套筒后,再将螺母旋进1/4圈,求螺栓与套筒间的预紧力。
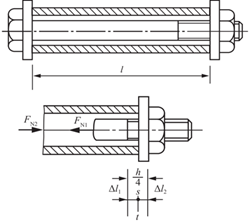
图2-2-66
解:把螺母再旋进1/4圈,螺栓受拉而套筒受压。将螺栓及套筒切开,并以FN1和FN2表示螺栓的拉力和套筒的压力,平衡方程为
FN1-FN2=0①
如图2-2-66所示变形之间的关系应为
Δl1+Δl2=h/4②
Δl1和Δl2皆为绝对值。设钢螺栓的抗拉钢度为E1A1,铸铁套筒的抗压刚度为E2A2,由胡克定律,得
Δl1=FN1l/(E1A1),Δl2=FN2l/(E2A2)
于是式②化为
FN1l/(E1A1)+FN2l/(E2A2)=h/4③
由式①③可得
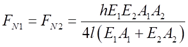
2.47 如图2-2-67所示阶梯形钢杆的两端在T1=5℃时被固定,杆件上下两段的横截面面积分别是A上=500mm2,A下=1000mm2。钢材的αl=12.5×10-6℃-1,E=200GPa。当温度升高至T2=25℃时,试求杆内各部分的温度应力。
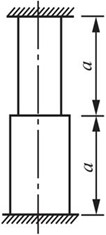
图2-2-67
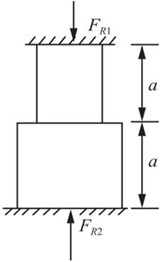
图2-2-68
解:如图2-2-68所示,钢杆必受压,且由受力平衡可知:FR1=FR2。
在温度影响下,钢杆变形量:Δl=αlΔT。
在两端支反力作用下,钢杆的压缩变形量:Δl′=Δl1+Δl2。
则变形协调方程:Δl=Δl′。
由胡克定律上式可变形为:αlΔT=FRa/(EA上)+FRa/(EA下)。
解得:
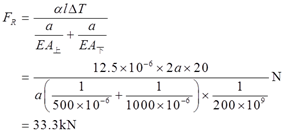
故上下两部分的温度应力分别为
σ上=FR/A上=33.3×103/(500×10-6)=66.6MPa(压应力)
σ下=FR/A下=33.3×103/(1000×10-6)=33.3MPa(压应力)
2.48 如图2-2-69所示杆系的两杆同为钢杆,E=200GPa,αl=12.5×10-6℃-1。两杆的横截面面积同为A=1000mm2。若BC杆的温度降低20℃,而BD的温度不变,试求两杆的应力。
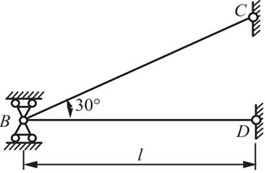
图2-2-69
解:对节点B进行受力分析,如图2-2-70(b)所示。
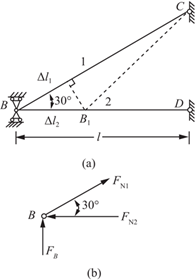
图2-2-70
由平衡条件可得:∑Fx=0,FN1cos30°-FN2=0①
又根据变形作位移图,如图2-2-70(a)所示,可得变形协调条件
Δl1=Δl2cos30°②
由胡克定理可得:Δl2=FN2l2/(EA)。
又杆BC在温度变化和轴力FN1共同作用下的变形量
Δl1=αl1ΔT-FN1l1/(EA)
则代入式②可得
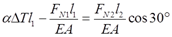 ③
③
联立式①③可得
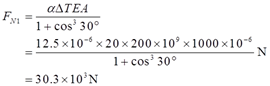
FN2=FN1cos30°=26.2×103N
故两杆的应力分别为
σ1=FN1/A1=30.3×103/(1000×10-6)Pa=30.3MPa(拉)
σ2=FN2/A2=26.2×103/(1000×10-6)Pa=26.2MPa(压)
2.49 在图2-2-71所示结构中,1,2两杆的抗拉刚度同为E1A1,3杆为E3A3。3杆的长度为l+δ,其中δ为加工误差。试求将3杆装入AC位置后,1,2,3三杆的轴力。
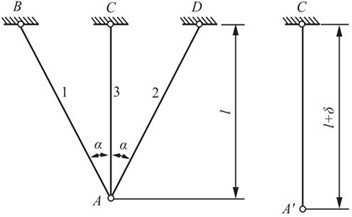
图2-2-71
解:如图2-2-72所示,分析节点A处受力,并作出变形后节点A的位移图。
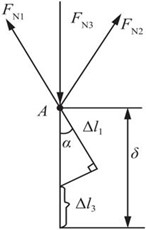
图2-2-72
由平衡条件可得
∑Fy=0,(FN1+FN2)cosα-FN3=0①
∑Fx=0,FN2sinα-FN1sinα=0②
变形协调条件:Δl1/cosα+Δl3=δ。
由胡克定律上式可变形为:FN1l1/(E1A1cosα)+FN3l/(E3A3)=δ③
联立式①②③可得各杆轴力
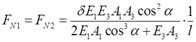
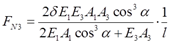
2.50 图2-2-73所示杆系的杆6比名义长度略短,误差为δ,所有杆的刚度同为EA,试求装配后各杆的轴力。
提示:解除杆6,并将它的内力FN6作用于A和C两节点。借用题2.32的方法,求出A,C两点沿AC方向的位移uA和uC。若再以Δl6表杆6的伸长,则变形协调方程应为
uA+uC+Δl6=δ
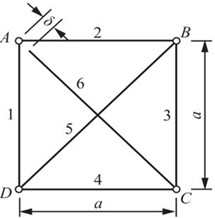
图2-2-73
解:解除杆6,并以它的内力作用于A、C两节点,如图2-2-74所示。
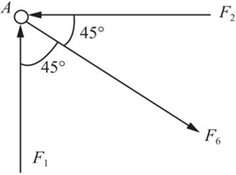
图2-2-74
由载荷和结构的对称性,根据平衡条件可知各杆的轴力
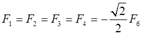
F5=F6
解法一:则该杆系总的应变能
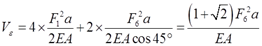
根据功能原理知:
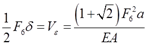
解得:F6=0.207EAδ/a。
故各杆轴力
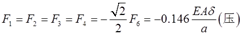
F5=F6=0.207EAδ/a(拉)
解法二:变形协调方程为uA+uC+Δl6=δ。
根据题2.32的结论,有
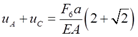
代入变形协调方程
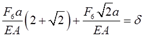
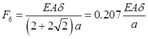
故各杆轴力为
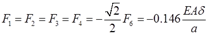
F5=F6=0.207EAδ/a
2.51 在图2-2-75所示杆系中,AB杆比名义长度略短,误差为δ。若各杆材料相同,横截面面积相等,试求装配后各杆的轴力。
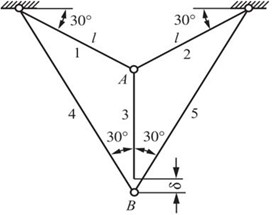
图2-2-75
解:分别对节点A、B进行受力分析,如图2-2-76所示。
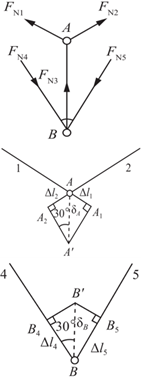
图2-2-76
由结构和载荷的对称性及平衡条件可得
FN1=FN2=FN3,FN4=FN5①
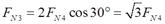 ②
②
装配后,在杆3轴力作用下,点A下移δA,点B向上移动δB,杆3的伸长变形量Δl3,则变形协调方程:δA+δB+Δl3=δ③
由图2-2-76所示几何关系及胡克定律可得
δA=Δl1/sin30°=2Δl1=2FN1l/(EA)
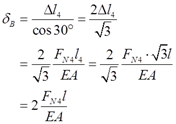
且Δl3=FN3l3/(EA)=FN3l/(EA)。
则式③可变形为:2FN1l/(EA)+2FN4l/(EA)+FN3l/(EA)=δ。
整理得:2FN1+2FN4+FN3=EAδ/l④
联立式①②④可得各杆内力
FN1=FN2=FN3=0.241EAδ/l(拉)
FN4=FN5=0.139EAδ/l(压)
2.52 杆1为钢杆,E1=210GPa,αl1=12.5×10-6℃-1,A1=3000mm2。杆2为铜杆,E2=105GPa,αl2=19×10-6℃-1,A2=3000mm2。载荷F=50kN。若AB为刚杆,且始终保持水平,试问温度是升高还是降低?并求温度的改变量ΔT。
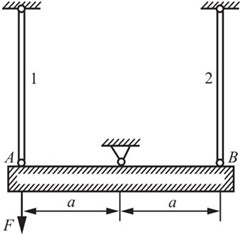
图2-2-77
解:对刚杆AB进行受力分析,如图2-2-78所示。
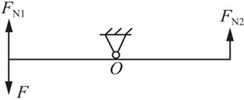
图2-2-78
由平衡方程∑M0=0,FN2a+Fa-FN1a=0,可得
F=FN1-FN2①
设温度上升ΔT,刚杆AB能够始终保持水平,则可得协调方程
Δl1+Δl1T=0,Δl2+Δl2T=0②
由胡克定律可得因轴力引起的伸长量:Δl1=FN1l1/(E1A1),Δl2=FN2l2/(E2A2)。
由温度上升引起的压缩量:Δl1T=αl1ΔTl1,Δl2T=αl2ΔTl2。
代入式②可得:FN1+αl1E1A1ΔT=0,FN2+αl2E2A2ΔT=0③
联立式①③得:ΔT=F/(αl2E2A2-αl1E1A1)。
即
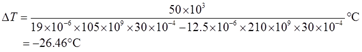
负号表示与假设相反,温度降低26.46°即可保证刚杆AB保持水平。
*2.53 如图2-2-79所示,刚性横梁AB悬挂于三根竖直杆上。l=2m,F=40kN,a=1.5m,b=1m,c=0.25m,δ=0.2mm。1杆由黄铜制成,A1=200mm2,E1=100GPa,αl1=16.5×10-6℃-1。2杆和3杆由碳钢制成,A2=100mm2,A3=300mm2,E2=E3=200GPa,αl2=αl3=12.5×10-6℃-1。设温度升高20℃,试求各杆横截面上的应力。
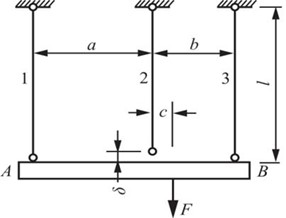
图2-2-79
解:对刚性横梁AB进行受力分析,如图2-2-80所示。
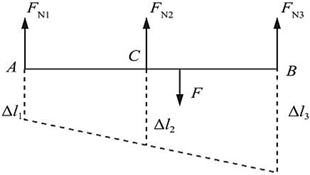
图2-2-80
由平衡条件可得
∑Fy=0,FN1+FN2+FN3-F=0①
∑MC=0,FN1a+Fc-FN3b=0②
由图中几何关系可得变形协调方程:b/(a+b)=(Δl3-Δl2)(Δl3-Δl1)③
其中在温度变化和轴力共同作用下,各杆变形量
Δl1=αl1ΔTl1+FN1l1/(E1A1),Δl2=αl2ΔTl2+FN2l2/(E2A2)-δ,Δl3=αl3ΔTl3+FN3l3/(E3A3)④
联立式①②③④,可得各杆内力
FN1=7.92kN,FN2=10.2kN,FN3=21.9kN
故各杆应力
σ1=FN1/A1=7.92×103/(200×10-6)Pa=39.6MPa
σ2=FN2/A2=10.2×103/(100×10-6)Pa=102MPa
σ3=FN3/A3=21.9×103/(300×10-6)Pa=73MPa
*2.54 如图2-2-81所示,两端固定的杆件,横截面面积A=1200mm2,a=300mm。材料的应力一应变关系见题2.25图2-2-33(b)。试分别求F=60kN和F=210kN时,杆件上下两段横截面上的应力。
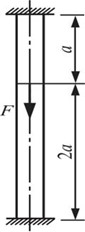
图2-2-81
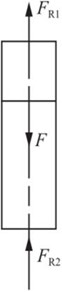
图2-2-82
解:如图2-2-82所示,由平衡方程可得:F=FR1+FR2①
变形协调方程:Δl1=Δl2②
由应力—应变曲线可得,转折点处对应的内力值
F=σA=100×106×1200×10-6N=120kN
(1)F=60kN<120kN时,根据胡克定律,式②变形为
FR1a/(EA)=2FR2a/(EA)③
联立式①③得:FR1=2F/3,FR2=F/3。
则各段应力
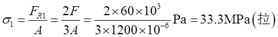
σ2=FR2/A=F/(3A)=16.7MPa(压)
(2)F=210kN>120kN时,应分段计算变形量,先假设FR2<120kN,此时根据胡克定律式②变形为
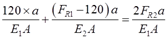 ④
④
联立式①④得:FR1=126.7kN,FR2=83.3kN<120kN,假设成立,上述等式可用。
则各段应力
σ1=FR1/A=126.7×103/(1200×10-6)Pa=105.6MPa(拉)
σ2=FR2/A=83.3×103/(1200×10-6)Pa=69.4MPa(压)
2.55 试确定图2-2-83中连接或接头中的剪切面和挤压面
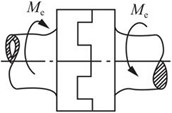
图2-2-83(a)
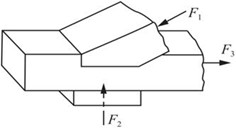
图2-2-83(b)
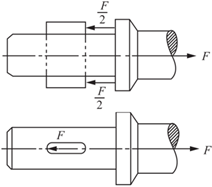
图2-2-83(c)
解:如图2-2-84(a)所示,AB、CD、B′C′为剪切面,BB′、CC′、DD′为挤压面;
如图2-2-84(b)所示,AB面为剪切面,BC面为挤压面;
如图2-2-84(c)所示,AB、CD面为剪切面,E面为挤压面。
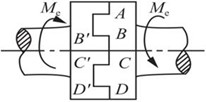
图2-2-84(a)
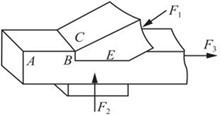
图2-2-84(b)
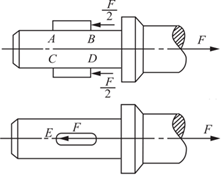
图2-2-84(c)
2.56 如图2-2-85所示销钉连接中。已知F=100kN,销钉直径d=30mm,材料的许用切应力[τ]=60MPa。试校核销钉的剪切强度。若强度不够,应改用多大直径的销钉?
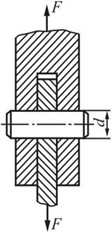
图2-2-85
解:图2-2-86为销钉受力图,其两个剪切面受到的剪切力均为FS=F/2。
则该销钉的切应力
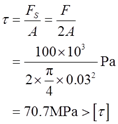
由此可知该销钉强度不够。
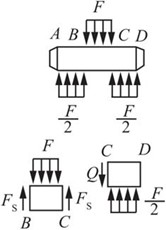
图2-2-86
由强度条件
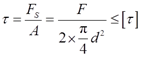
可得
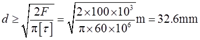
即应改选用直径d≥32.6mm的销钉。
2.57 测定材料剪切强度的剪切器的示意图如图2-2-87所示。设圆试样的直径d=15mm,当压力F=31.5kN时,试样被剪断,试求材料的名义剪切极限应力。若取剪切许用应力为[τ]=80MPa,试问安全因数等于多大?
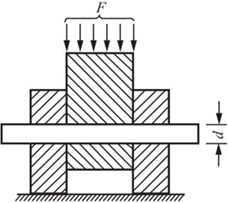
图2-2-87
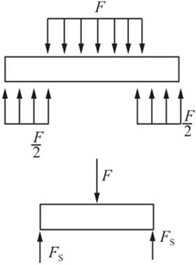
图2-2-88
解:如图2-2-88所示,由试件受力部分的分析可知,试件横截面上承受的剪力FS=F/2。
该试件的名义剪切极限应力
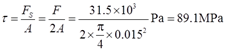
由许用应力的定义[τ]=τu/n,可得安全系数:n=τu/[τ]=89.1/80=1.1。
2.58 如图2-2-89所示,凸缘联轴节传递的力偶矩为Me=200N·m,凸缘之间用四根螺栓连接,螺栓内径d≈10mm。对称地分布在直径为80mm的圆周上。如螺栓的剪切许用应力[τ]=60MPa,试校核螺栓的剪切强度。
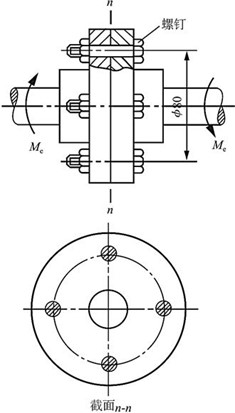
图2-2-89
解:4个螺栓均匀承受由外力偶矩引起的剪力,且为F,则由平衡条件Me=4FD0/2,得
F=Me/(2D0)=200/(2×80×10-3)N=1.25kN
则每个螺栓内的剪应力:
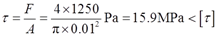
故螺栓满足强度要求,是安全的。
2.59 一螺栓将拉杆与厚为8mm的两块盖板相连接,如图2-2-90所示。各零件材料相同,许用应力均为[σ]=80MPa,[τ]=60MPa,[σbs]=160MPa。若拉杆的厚度δ=15mm,拉力F=120kN,试设计螺栓直径d及拉杆宽度b。
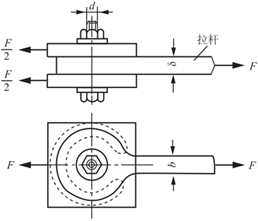
图2-2-90
解:(1)确定螺栓直径
①由剪切强度条件
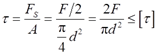
可得
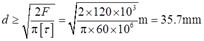
②由挤压强度条件σbs=F/Abs=F/(dδ)≤[σbs],可得
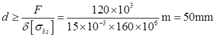
综上,取较大值螺栓直径取d≥50mm。
(2)确定拉杆宽度
由拉杆拉伸强度条件σ=F/(bδ)≤[σ],可得
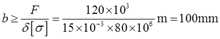
故拉杆宽度取b≥100mm。
2.60 图2-2-91所示的机床花键轴有8个齿。轴与轮的配合长度l=60mm,外力偶矩Me=4kN·m。轮与轴的挤压许用应力为[σbs]=140MPa,试校核花键轴的挤压强度。
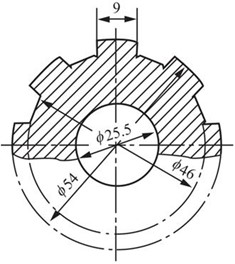
图2-2-91
解:假设挤压力均匀作用在8个挤压面上,并设每个面的挤压力的合力为F,则有
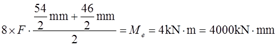
解得:F=20kN。
则挤压应力
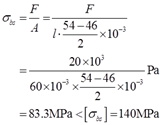
故花键轴的挤压强度满足要求,是安全的。
2.61 在厚度δ=5mm的钢板上,冲出一个形状如图2-2-92所示的孔,钢板剪断时的剪切极限应力τu=300MPa,求冲床所需的冲力F。
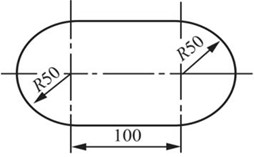
图2-2-92
解:钢板被剪断时,剪应力需满足:τ=F/A≥τu。
其中剪切面面积:A=(2πR+2l)δ。
故冲床所需冲力
F≥τuA=300×106×(2π×0.05+2×0.1)×0.005N=771kN
2.62 可倾式压力机为防止过载采用了压环式保险器(如图2-2-93所示)。当过载时,保险器先被剪断,以保护其他主要零件。设压环式保险器以剪切的形式破坏,且剪切面的高度δ=20mm,材料的剪切极限应力τu=200MPa,压力机的最大许可压力F=630kN。试确定保险器剪切部分的直径D。
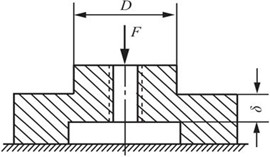
图2-2-93
解:保险器剪断时有剪应力τ=F/A≥τu,其中剪切面面积A=πDδ,则有
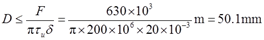
即保险器剪切部分的直径不超过50.1mm。
2.63 车床的传动光杆装有安全联轴器,如图2-2-94所示,当超过一定载荷时,安全销即被剪断。己知安全销的平均直径为5mm,材料为45钢,其剪切极限应力为τu=370MPa。求安全联轴器所能传递的力偶矩Me。
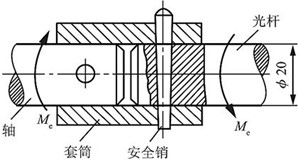
图2-2-94
解:安全销的剪切面上能承受的最大剪力
FS=τuA=τuπd2/4=370×106×(π/4)×(5×10-3)2N=7264.9N
所以安全联轴器能传递的最大力偶矩
Me=FS·D=7264.9×20×10-3N·m=145N·m
2.64 图2-2-95所示螺钉在拉力F作用下。己知材料的剪切许用应力[τ]和拉伸许用应力[σ]之间的关系约为:[τ]=0.6[σ]。试求螺钉直径d与钉头高度h的合理比值。
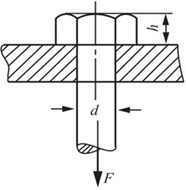
图2-2-95
解:螺栓的拉应力:σ=F/A=4F/(πd2)。
钉头的切应力:τ=F/A′=F/(πdh)。
当螺栓和钉头的应力同时达到许用应力值时,d/h值达到最合理,即
σ=4F/(πd2)=[σ],τ=F/(πdh)=[τ]
比较可得:d/(4h)=[τ]/[σ]=0.6,即d/h=2.4。
故螺钉杆直径d与钉头高度h的合理比值为2.4。
2.65 木榫接头如图2-2-96所示。α=b=120mm,h=350mm,c=45mm,F=40kN。试求接头的剪切和挤压应力。
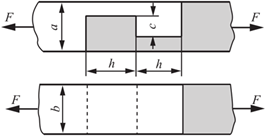
图2-2-96
解:接头的剪切应力:
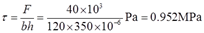
挤压应力:
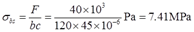
2.66 用两个铆钉将140mm×140mm×12mm的等边角钢铆接在立柱上,构成支托,如图2-2-97所示。若F=30kN,铆钉的直径为21mm,试求铆钉的切应力和挤压应力。
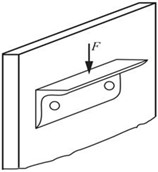
图2-2-97
解:由结构和载荷的对称性,假设每个铆钉的剪切力均为F/2,则切应力
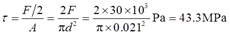
铆钉的每个挤压面为其与角钢相接触的圆柱面,则挤压应力
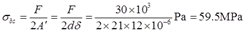
2.67 用夹剪剪断直径为3mm的铅丝,如图2-2-98所示。若铅丝的剪切极限应力约为100MPa,试问需要多大的F?若销钉B的直径为8mm,试求销钉内的切应力。
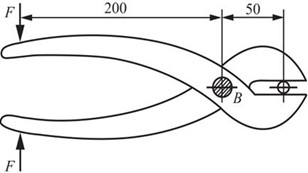
图2-2-98
解:铅丝剪断时,其所承受的剪力
FS=τuA=τuπd2/4=100×106×(π/4)×(3×10-3)2N=706.86N
如图2-2-99所示,对夹剪进行受力分析,由其对称性,分析一半即可。
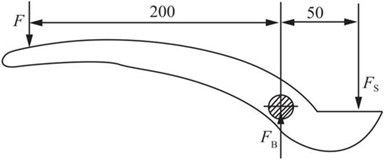
图2-2-99
由平衡条件
∑MB=0,-F×200+FS×50=0
∑Fy=0,FB-FS-F=0
可得:F=FS/4=176.7N,FB=883.57N。
故销钉B内的切应力:
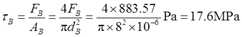
2.68 如图2-2-100所示,柴油机的活塞销材料为20Cr,[τ]=70MPa,[σbs]=100MPa,活塞销外径d1=48mm,内径d2=26mm,长度l=130mm,a=50mm,活塞直径D=135mm。气体爆发压力p=7.5MPa。试对活塞销进行剪切和挤压强度校核。
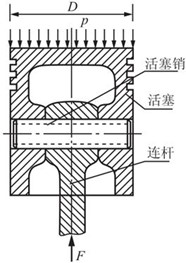
图2-2-100(a)
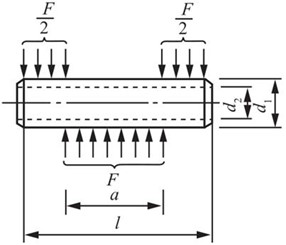
图2-2-100(b)
解:如图2-2-100(b)所示,气体爆发作用在活塞上的压力均匀分布,值为
F=pπD2/4=7.5×106×(π/4)×0.1352N=107kN
①剪切强度校核
如图2-2-100(b)所示,活塞销每个剪切面上的剪力为F/2,且活塞受剪切的横截面面积为A=π(d12-d22)/4,则其剪应力
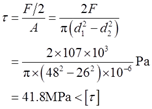
故剪切强度满足要求。
②挤压强度校核
活塞销两端受活塞挤压,挤压面积为A=d1·(l-a)/2,则挤压应力
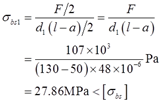
活塞中间段受连杆挤压,挤压面积为A=d1·a,则挤压应力
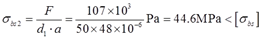
综上,活塞销挤压强度也满足要求,是安全的。
